测试你的数学技巧

眼力挑战玩法深受部分玩家喜欢，这种沉浸式找不同的玩法确实很有吸引力，比如最近的测试你眼力这款游戏，喜欢益智类玩法的玩家一定不要错过它，那么测试你的眼力下载途径是什么呢？这不，小编已经准备好了相关链接并且贴在了文章中，玩家点击查看就会跳转哦。

《测试你的眼力》最新预约下载地址：

》》》》》#测试你的眼力#《《《《《

测试你的眼力这款游戏还没有上线哦，但是玩家可以点击上方链接预约起来。

在扁平化视觉风格中，玩家将全身心投入到眼力挑战中。挑战模式是非常多样的，玩家既可以在普通关卡中训练自己的眼速，也可以在难度比较高的关卡中快速找出物体的不同，有些关卡则需要玩家动脑子进行辨别并且快速做出选择。所有的关卡都没有时间限制，玩家在保证正确的前提下进行操作。随着关卡的升级，即便是同一类型的考验眼力的玩法，难度也会有所上升，不过玩家不用担心，系统会有一定的提示功能，玩家可以根据提示通过关卡。无论是哪一种挑战模式，玩家都可以使用提示功能，当关卡中的格子会自己动起来的时候，玩家就可以点击该格子来获得提示，每一关卡中的提示次数没有限制，这种自动提示功能对新手玩家非常友好的。

最为经典的玩法类似于排雷。每一个关卡页面的中心会出现格子盘，在不同的关卡中，玩家看到的格子盘是不一样的，随着关卡的进行，格子盘中的格子数量会越来越多，整个游戏难度也会越来越大，这个时候就很容易犯错，各位玩家要小心哦。在具体操作方面，玩家点击格子盘中的任意一个格子，该格子翻面之后会出现数字，数字是1到8之间，该数字就代表着以该格子为中心的9个格子里面有几个炸弹，玩家根据已有信息进行判断，并且将炸弹区插上小红旗进行标识，当关卡中的所有炸弹区被找出来后，玩家就可以通关了。在其他的玩法当中，玩家也可以得到眼力的增长。

好啦，以上就是测试你的眼力下载的分享内容啦，测试眼力的玩法内容是比较丰富的，有的玩法比较考验玩家的观看速度，而有的重在观察物体之间的不同，在不同的玩法中，玩家的眼力会得到不同层次的训练，各位玩家一起来体验一下这块眼力游戏吧。

最近有很多小伙伴在问测试你的眼力下载去哪里方便，这是一款体量非常小的休闲游戏，可以给大家在休闲时带来很多乐趣。游戏的核心玩法非常简单，就是盯着图片看然后找出不对劲的地方，和大家之前玩过的很多找茬小游戏非常相似，如果感兴趣就一起往下看吧。

【测试你的眼力】最新版预约/下载地址

》》》》》#测试你的眼力#《《《《《

上面的链接可以直接点击去九游预约游戏，因为还没有开放正式服务器，暂时不能下载，预约之后就能及时收到消息了。选择九游是因为这是手游福利最好的APP，节假日有万元无门槛券免费抽福利，零元也能畅玩。开张省钱卡就能每月自动获得60元券，全年一共720元。游戏玩法非常简单，进入关卡后会看到一张看似正常的图片，需要仔细审查画面中的每一个角落，找出其中不合理的部分。

这里注意并不是找不同，而是找不合理。不合理的原因有很多，有可能是某个物品出现在不该出现的地方，也有可能是颜色、形状和位置比较违和，所以游戏虽然考验眼力，但也很考验逻辑判断。在发现异常之后，点击对应位置就可进行标记，把当前关卡图片中的所有异常点都找出来，就可以通关进入到下一关。

初期比较简单，就是为了让大家培养寻找的感觉，以及明白到底哪些是不合理。随着关卡推进，异常点会越来越隐蔽，对观察力的考验也会逐步升级。所以游戏和传统找茬类有着很大的区别。

看完上面的介绍之后，大家现在就清楚测试你的眼力下载去哪里方便了吧。现在加入九游就能参加暑假活动，活动时间从7月10日一直到8月31日，一起来翻出你的暑假免单，九游1万元大奖等你来挑战。

期待已久的手游测试你的眼力即将登陆九游，这款手机游戏吸引了大批玩家的关注，想下载这款游戏，有很多粉丝都在问九游小编测试你的眼力好玩吗？测试你的眼力值不值得玩？现在就为大家来简单分析下，看看这款游戏的玩法特点和游戏剧情介绍 。

测试你的眼力快速预约/下载地址（需优先下载九游APP）：

》》》》》#测试你的眼力#《《《《《

1、测试你的眼力简要评析：

这个游戏中好像有点不对劲

2、测试你的眼力图片欣赏：

通过上面的游戏介绍和图片，可能大家对测试你的眼力有大致的了解了，不过这么游戏要怎么样才能抢先体验到呢？不用担心，目前九游客户端已经开通了测试提醒了，通过在九游APP中搜索“测试你的眼力”，点击右边的【订阅】或者是【开测提醒】，订阅游戏就不会错过最先的下载机会了咯！

关键字：可口的披萨美味的披萨数学测试怎么过 数学测试通关方法

LOL测试你的最佳队友，看看谁才是你的最佳队友！下面小编为大家带来了测试你的最佳队友活动网址，赶快来测试一下吧！

使用方法：

1.登录自己的帐号，选择大区后确定角色。

2.点击查询，就可以测试谁才是你的最佳队友了！

小编测试：

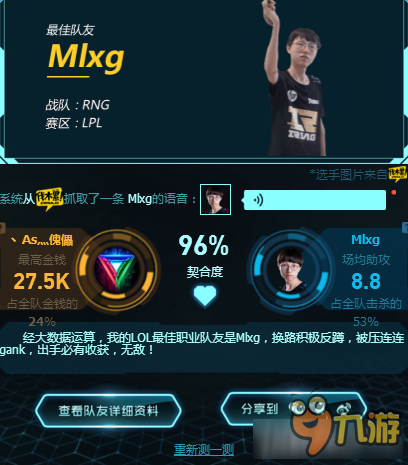
看了上边这篇LOL最佳队友测试，各位玩家是否都了解相关信息了呢！找精彩好玩手机游戏请浏览九游。

如转载涉及版权等问题，请作者与我司联系，我司将在第一时间删除或支付稿酬。

现在有一种说法，手游智商低龄化，越来越多的全自动、挂机型手游的出现，让每一名玩家玩游戏的时候不需要动脑子，有的甚至连手都不需要动了，这究竟是游戏的进步还是游戏的悲哀？

游戏的进步，始终是在玩法上，轻松简单的游戏容易上手容易火，但不代表脑残游戏也能火，在目前游戏有往脑残简单化发展的趋势下，一款好的动脑子的游戏非常稀有，可以说还愿意做一款用智商获胜的游戏，一定是游戏的真爱粉。

说到动脑子，我们第一想到的游戏术语肯定是“大局观”，或者叫做策略。凡是经典游戏，都离不开“策略”两个子， 总体来说是要靠动脑子来取得游戏的胜利。再者，棋类通常都是要动脑子的，战棋类游戏不用说，想挂机没门，想不动脑子没门。那么，作为策略战棋类游戏，《仙境骑士团》狠狠得秀了一把智商，这是一款非常需要动脑的游戏，想轻松想挂机的千万别玩！

战棋这两个字就限定了，玩这个游戏走位肯定处于非常重要的位置，向哪里走，走几步，都是决定胜负的要素。再者，策略战棋，加了一个策略前缀，就表示光会走位也不能完全胜任，还要学会懂脑子，比如战队职业的搭配，技能释放的时机，开场阵型站位等，都不能无视，任何一处改变都可能改变战局。

《仙境骑士团》作为首款策略战棋类游戏，不仅继承了经典端游仙境传说RO的画面、职业，地图，还特别设定了新的剧情，新的副本，每一个关卡需要你去探索，只有战胜敌人，才能获得关卡里隐藏的财富。

相信每一关副本里设定的挑战，肯定会让大家多动脑筋，用属于你们的策略智慧战胜敌人，完成探险！来吧，考验智商的《仙境骑士团》即将登场，欢迎您加入这片需要探索的世界，测试你的智商高不高！