我爱数学游戏介绍
我爱数学简介
我爱数学好玩吗 我爱数学玩法简介
期待已久的手游我爱数学即将登陆九游,这款手机游戏吸引了大批玩家的关注,想下载这款游戏,有很多粉丝都在问九游小编我爱数学好玩吗?我爱数学值不值得玩?现在就为大家来简单分析下,看看这款游戏的玩法特点和游戏剧情介绍 。
我爱数学快速预约/下载地址(需优先下载九游APP):
》》》》》#我爱数学#《《《《《
1、我爱数学简要评析:
再固定时间内快速计算数学题,选出正确答案。
2、我爱数学图片欣赏:

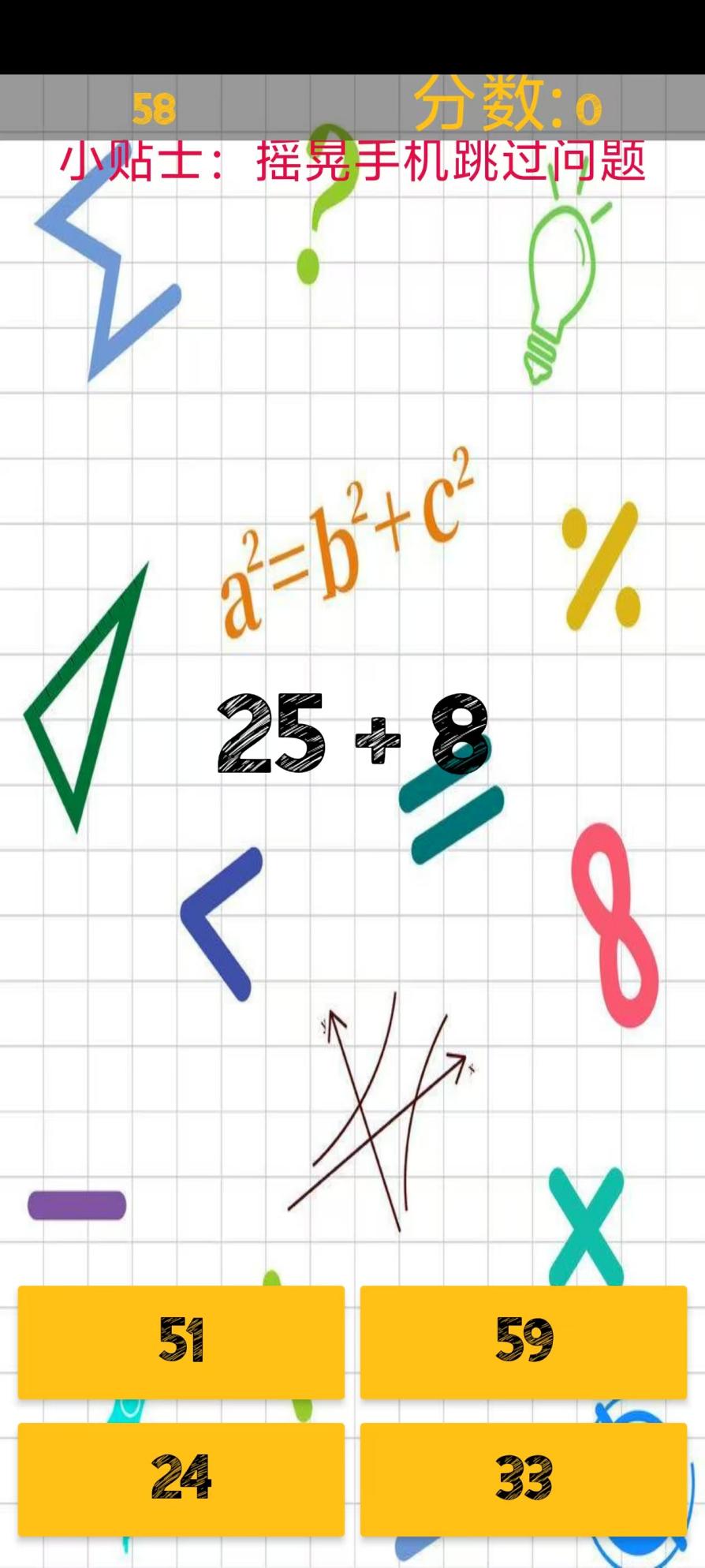

通过上面的游戏介绍和图片,可能大家对我爱数学有大致的了解了,不过这么游戏要怎么样才能抢先体验到呢?不用担心,目前九游客户端已经开通了测试提醒了,通过在九游APP中搜索“我爱数学”,点击右边的【订阅】或者是【开测提醒】,订阅游戏就不会错过最先的下载机会了咯!
 全球好游抢先下
全球好游抢先下 福利礼包免费领
福利礼包免费领 官方直播陪你玩
官方直播陪你玩
我爱数学什么时候出 公测上线时间预告
导读:最近很多玩家都在关注我爱数学这款手游,想知道具体的公测时间,我爱数学会经过封测、删档内测、不删档测试到最终的公测等几个测试阶段,才会正式上线我爱数学安卓或iOS版本,有很多玩家就会问小编我爱数学什么时候公测,究竟什么时候出呢?今天小编就为大家提供如何快速地知道我爱数学开放下载和公测的时间,你就可以最快知道我爱数学公测时间了!
我爱数学快速预约/下载地址(需优先下载九游APP):
》》》》》#我爱数学#《《《《《

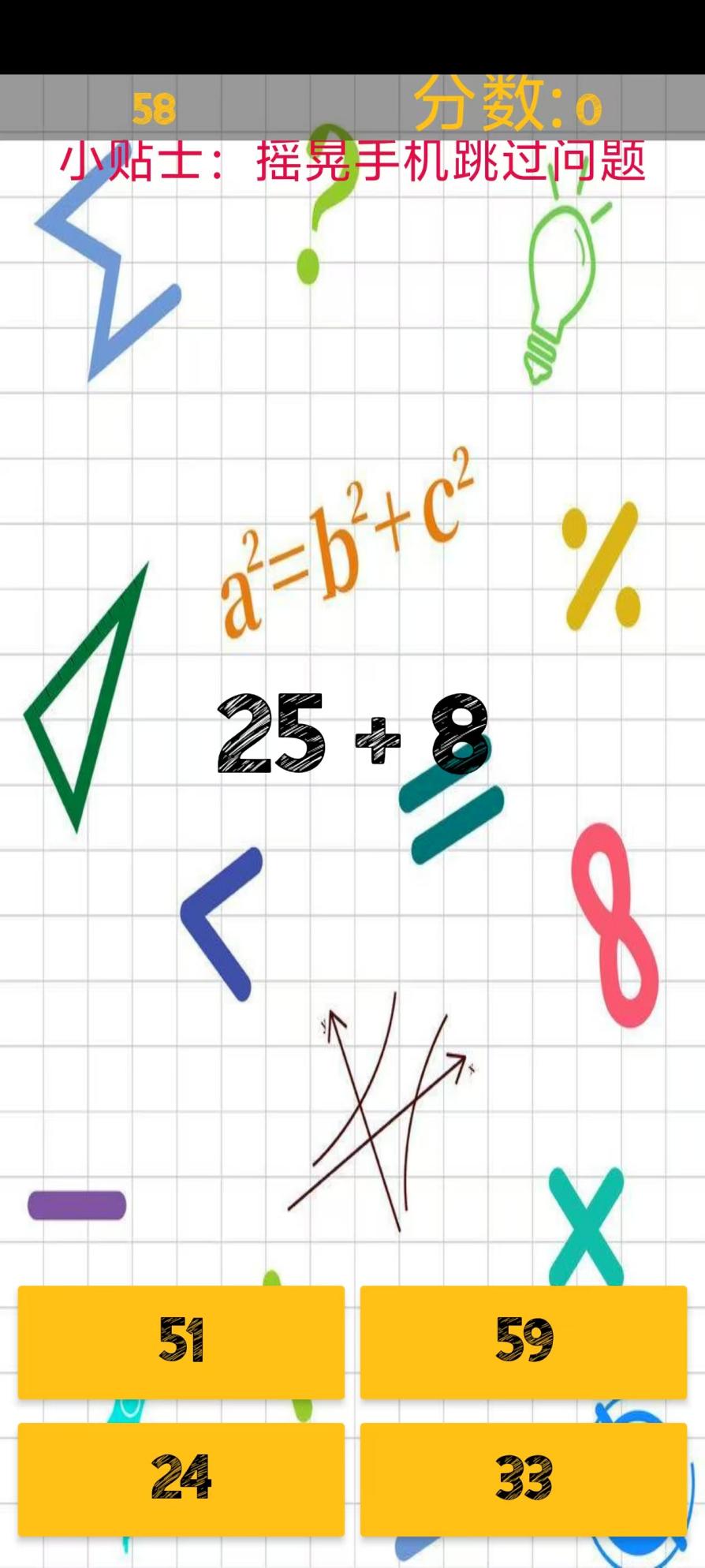

我爱数学什么时候公测?公测时间提前预知,有三大方法,下边就让九游独家来为您揭秘吧!
方法一: 关注九游我爱数学大事件
步骤1:百度搜索 “九游我爱数学” 专区;
步骤2:关注大事件列表,每次我爱数学测试的时间都会最新发布,这是九游独家的哦;
方法二: 下载九游APP,订阅我爱数学的开测提醒
步骤1:点击下载九游APP;
步骤2:进入APP搜索“我爱数学”,订阅后可及时接受活动,礼包,开测和开放下载的提醒;
 全球好游抢先下
全球好游抢先下 福利礼包免费领
福利礼包免费领 官方直播陪你玩
官方直播陪你玩
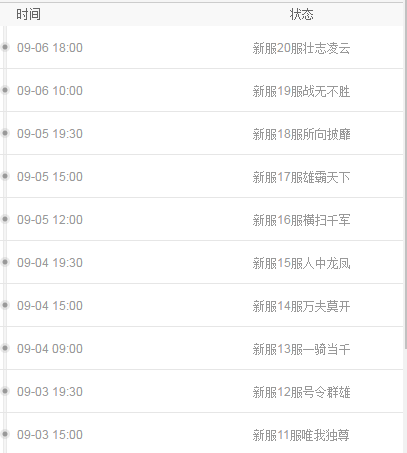
方法三: 查看九游开测表
步骤1:在九游开测表中玩家们可以看到当天所有进行开测的手机游戏,以及最近十天即将进行测试的游戏,有具体的测试时间以及测试阶段介绍,玩家们可以在这里查找我爱数学的相关公测时间信息!
步骤2:访问地址>>>手游开测表地址
好了,我爱数学公测时间的关注方法就讲到这里,各位玩家是否都已经掌握好以上三种技巧了呢,随时随地关注我爱数学什么时候开测,什么时候开放下载,什么时候公测等信息,还有一个办法就是留意九游我爱数学专区的每日更新,欢迎大家积极参与讨论和提问题,我们会第一时间为您解答。
我爱数学官网在哪下载 最新官方下载安装地址
我爱数学怎么下载?想要比别人更加抢先抢快的玩到这款游戏,那么你获取游戏开测消息是关键,能够获取到第一手信息,你才能在最快的时间内容体验到,我爱数学怎么下载呢?在哪里可以免费下载?下面九游小编为你带来两招,轻松解决你的烦恼,告诉你在哪里可以下载我爱数学安卓2022最新版。
我爱数学快速预约/下载地址(需优先下载九游APP):
》》》》》#我爱数学#《《《《《
点击进入九游门户,搜索我爱数学,进入之后你会看到一个下载按钮,分别是【高速下载】和【下载】,高速下载可以更加节省下载时间和流量,能够很好的解决下载耗时长的问题。如图所示:

最直接的方法就是到九游APP进行下载,九游APP提供海量的精品游戏下载,
在九游客户端搜索栏中输入我爱数学进行搜索,点击进入到游戏专区中,如图所示:如图所示,这样你就不用四处寻求游戏下载包,简简单单的两步你就可以安装了,同时还有大量的安卓手机游戏攻略。
九游APP下载【高速下载】

好了,小编为大家大家提供了这两种教程是下载我爱数学最为直接方法哦,不知道大家有没有清楚的知道呢?想要了解更多精彩内容,不妨多多关注九游我爱数学
我爱数学游戏截图




大家都在看-热门推荐
我数学特强《我数学特强》通解是存在的
我数学特强《我数学特强》通解是存在的!如下:
《我数学特强》有没有万能公式呢?很久之前,一开始玩的时候,就想过这个问题,但面对复杂的变换路径,我完全没有头绪。
最近的研究让我找到了通用的解法,这不是用程序暴力搜索答案,也不是简要的技巧,而是公式化的解法。另外,游戏里要求使用最少步数的最优解,而通解一般不限步数。
介绍一下游戏。有三个自然数,玩家每次操作可以对这三个数进行分配,我称为偶变换和奇变换,偶变换是把一个偶数减半并将减半的部分加到另一个数上,奇变换是把一个奇数加到另一个数上,然后将其变为0。实际上,奇变换不限奇数,因为将偶数奇变换给另一个数,可以先一直偶变换直到变为奇数,再进行奇变换。游戏的最终目标是得到三个相等的数,用三元数组表示为{x, x, x},不过显然只要三个数里有x或2x就能得到{x, x, x}。
有通解的前提是有解,而有解的充要条件是,三个数的最大公约数g整除x(可表示为g|x),且三个数不是一零二奇。先证明必要性,og和og'分别为三个数变换前后的最大奇公约数,易证og|og',如果og'=x,则og|x,也就是说如果得到了{x,x,x},则有og|x,因此og|x是有解的必要条件。另外,由g=(a,b,c)(三个数a,b,c的最大公约数写法为(a,b,c)),可得g|3x,令g=og*2^m,则(og*2^m)|3x,(2^m)|(3x/og),而(2^m,3)=1,所以(2^m)|(x/og),(og*2^m)|x,可得g|x也是有解的必要条件,其逆否命题为,若g不整除x,则无解,而(0,0,3x)不整除x,一零两奇时只能奇变换为{0,0,3x},两者等价,所以三数不是一零两奇也是有解的必要条件。至于充分性,如果我们找到了g|x且不是一零两奇情况下的解法,就相当于将其证明了。
通解讨论的数组默认已通过以上判别法筛选,以保证有解及证明充分性。但要注意,有解的数组在变换后不一定有解,通解的操作应当保证数组在变换后依然可解,时刻有g|x。
下面的是我早期想的通解,经过计算机验证,x为奇数时,x>17后出现反例:
一、有x或2x则结束。
三、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择三种操作进行后g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分配给两奇数使其变为两偶数,选择两种操作进行后g整除x的数组。
四、若数组中没有g*2^k满足g*2^k>=x,k是自然数,则不断在两正数之间进行偶变换(如果x是偶数,则需要保证两数都是偶数),如果找到g*2^k,则跳到步骤六。
五、在步骤四的循环中选择含有数被4整除得奇数(且该数减半小于x)的数组(如果x是偶数则选择被2整除的),将该数偶变换给0,再重新在两数之间不断进行偶变换(如果x是偶数,则需要保证两数都是偶数),出现g*2^k则结束,将另两个数合并。
六、用二进制数表示x/g,在左边补充0直到位数等于k,从最高位到最低位,若为1则将g*2^k分配给0(或者是步骤五中得到g*2^k一半的数),为0则分配给另一个数。这样就得到了x,结束。
虽然有很多漏洞,但大框架是对的。在下文逐步分析后,我们将会推导出一个正确的通解。
直接得到通解可能是困难的,于是我想着要不然先解决什么样的组合是可解的问题吧。反复观察变换路径后,我猜测g整除x应该和有解相关,并且还发现了og在变换的过程中不变或变大,而且变换后的og整除变换前的og。
然后,我再想的是解决相对简单的数组。在三个数之间变换是复杂的,暂未发现规律,所以我研究了只有一个数为0的数组。如果三个正数的数组都能转变为一零两正,那么通解问题就可以归约到一零两正如何变换出x或2x的问题。
我们需要保证三正变两正后,g依然满足g|x。如何操作呢?对于{a,b,c},奇变换后得到的{0,a+b,c}, {0,b,a+c}和{a,0,b+c}三个数组中,一定有一个数组的g满足g|x。
证明:3x的质因数分解为m*3^n,(m,n)=1。先假设三个数组的g都不整除x。(a+b,c)=(3x,c),(a+c,b)=(3x,b),(b+c,a)=(3x,a)如果都不整除x,则(3^n)|(a,b,c),又因为(a,b,c)|x,可得(3^n)|x,但3x=m*3^n,(m,3)=1,矛盾。
两奇一偶时(该偶数不为0),以上的三种操作可能会让数组变为一零两奇,因此我们要对该类情况作调整,它有两种变换:一、两奇相加;二、偶数拆分为两奇数,分别加给另外两奇数。这两种变换会使三正变一零两偶,且至少有一种使得g|x,证明类似上一个,不再赘述。这样的话,我们就将前面提到的可解的数组都转化为一零两正了。
前面说过{0,0,3x}是无解的,两个正数不能奇变换,那当然就只好偶变换了。当x为奇数时,两个数一奇一偶,偶变换的对象(即哪个数给另一个数一半)是确定的,得到的下一数组是唯一的。再加上数组的和是不变的,这样的数组个数有限,所以,经过有限次偶变换后,一定会回到原来的数组,形成偶变换循环。当x为偶数时,偶变换的路径是不唯一的,且不一定能不断偶变换,变换后还可能是一零两奇,比如{2,10}。x为偶数的这种情况,后续在改进偶变换的时候再提及。
我们的目标是在循环中找到t*2^k,t*2^k>=x,t|x,k>0,因为在有三个数时,将t*2^k偶变换分解,可以得到小于t*2^k任意一个自然数。但循环中并不一定有t*2^k(比如{5,28}),所以在早期的想法中,我想打破原有循环,把偶数偶变换分给第三个数,使得原来循环的两个数进入新的循环,以找到t*2^k。
在{a,b}的偶变换循环中,如果我们只关注其中一个数a,可以发现该数在作如下变换:偶数时减半,奇数时加上sum再减半,sum=a+b。冰雹猜想里的变换会迭代至2^k,而这里,迭代至t*2^k,a和sum要满足的所有条件是什么,是个open的问题。修改了几次进入新循环的方法后,程序依然发现反例。所以,探寻如何修正a和sum进入新的含有t*2^k的循环,这条路暂时行不通。
不小于x的t*2^k一定和小于x的t*2^k在同一循环中,找到其中一个便能找到其余的t*2^k。但要得到新的循环,就要将参与偶变换循环的两数之和sum减小,而最大的t*2^k满足t*2^k
这样我们就有一个新的思路,先找到小于x的t*2k,再保持t*2^k不变,将sum增大使得sum>2x,进行新一轮偶变换,得到不小于x的t*2^k。
在偶变换时,如果偶数减半后还是偶数,则将这一部分加到第三个数上,这样我们就将前面总和不变的循环改成了总和递减的。由于无论怎么变换三个数都必为自然数,循环的总和不能无限递减,那它的下界是多少呢?当不能再分配给第三个数时,总和不变,因此偶变换一次,对象就交换,此后的所有偶数除以2后都为奇数,假设(a,b)中a为偶数,此时偶数a的变换如下:
a
a/2
a/4+sum
a/8+sum/2
a/16+sum/4+sum
a/32+sum/8+sum/2
a/64+sum/16+sum/4+sum
...
第n个偶数和第n-1偶数的递推式为x_n+1=x_n/4+sum,x_0=a
可得通式x_n=(a-4sum/3)/4^n+4sum/3
当a>4sum/3时,x_n单调递增,当a<4sum/3时,x_n单调递减,数组的大小是有限的,不能单调递增或递减,因此a=4sum/3=2a/3+2b/3,可得a=2b,偶变换循环的过程中,a和b的最大奇公约数og始终不变,又因为b是奇数,b和2b的最大奇公约数为b,所以,当sum最小时,a=2b=2og。前面的三正变两正保持了g|x,所以b|x。
当x为奇数时,将{b,2b,3x-3b}转化为{b,3x-2b,0},再对两正数偶变换即可得到t*2^k<=3x<=t*2^(k+1),此时的t*2^k>=3x/2>x,可进行二进制分配。不过,我们不必操作至sum递减至3b,如果过程中出现了t*2^k,若其不小于x自然不用说,若小于x,则将另两个数合并再偶变换就能得到不小于x的。
当x为偶数时,3x-3b为奇数,如果a>=x,则a二进制分配即可得x,如果a
t*2^k>=(3x-b)/2>=5x/4>x。同样地,我们不一定要等sum减到3b,出现小于x的t*2^k时,t*2^k一定是循环中最大的,大于与它偶变换的奇数u,设第三个数为v,v是奇数,则由t*2^k
综上,我们得到了一个通解:
一、有x或2x则结束。
二、数组中是否有q=t*2^k,其中t|x,且q>x,k>0(第一次找到q或者q>x,需要将另两数合并),是则将q以外的另两个数合并,跳至六
三、是否q
四、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择其中g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分成奇数给两奇数,选择其中g整除x的数组。
五、进行步骤一二三,若偶变换的数不是偶数,则交换对象,一个偶数减半后,若参与偶变换的两个数不都是奇数,则不断进行偶变换,否则分配给第三个数(如果已经找到q则永远不再分配给第三个数),继续五。
六、用二进制数表示x/t,在左边补充0直到位数等于k,从最高位到最低位,若为1则将q分配给0,为0则分配给另一个数。这样就得到了x,结束。
至此,我们从理论上推导证明了通解的可行性,此外,我还写了验证该解法的cpp代码,对0<=x<=1000的所有有解数组都进行了验证并且验证成功。
当然,也许还存在其他通解,我很期待看到新想法。
我数学特强《我数学特强》通解是存在的
我数学特强《我数学特强》通解是存在的!如下:
《我数学特强》有没有万能公式呢?很久之前,一开始玩的时候,就想过这个问题,但面对复杂的变换路径,我完全没有头绪。
最近的研究让我找到了通用的解法,这不是用程序暴力搜索答案,也不是简要的技巧,而是公式化的解法。另外,游戏里要求使用最少步数的最优解,而通解一般不限步数。
介绍一下游戏。有三个自然数,玩家每次操作可以对这三个数进行分配,我称为偶变换和奇变换,偶变换是把一个偶数减半并将减半的部分加到另一个数上,奇变换是把一个奇数加到另一个数上,然后将其变为0。实际上,奇变换不限奇数,因为将偶数奇变换给另一个数,可以先一直偶变换直到变为奇数,再进行奇变换。游戏的最终目标是得到三个相等的数,用三元数组表示为{x, x, x},不过显然只要三个数里有x或2x就能得到{x, x, x}。
有通解的前提是有解,而有解的充要条件是,三个数的最大公约数g整除x(可表示为g|x),且三个数不是一零二奇。先证明必要性,og和og'分别为三个数变换前后的最大奇公约数,易证og|og',如果og'=x,则og|x,也就是说如果得到了{x,x,x},则有og|x,因此og|x是有解的必要条件。另外,由g=(a,b,c)(三个数a,b,c的最大公约数写法为(a,b,c)),可得g|3x,令g=og*2^m,则(og*2^m)|3x,(2^m)|(3x/og),而(2^m,3)=1,所以(2^m)|(x/og),(og*2^m)|x,可得g|x也是有解的必要条件,其逆否命题为,若g不整除x,则无解,而(0,0,3x)不整除x,一零两奇时只能奇变换为{0,0,3x},两者等价,所以三数不是一零两奇也是有解的必要条件。至于充分性,如果我们找到了g|x且不是一零两奇情况下的解法,就相当于将其证明了。
通解讨论的数组默认已通过以上判别法筛选,以保证有解及证明充分性。但要注意,有解的数组在变换后不一定有解,通解的操作应当保证数组在变换后依然可解,时刻有g|x。
下面的是我早期想的通解,经过计算机验证,x为奇数时,x>17后出现反例:
一、有x或2x则结束。
三、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择三种操作进行后g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分配给两奇数使其变为两偶数,选择两种操作进行后g整除x的数组。
四、若数组中没有g*2^k满足g*2^k>=x,k是自然数,则不断在两正数之间进行偶变换(如果x是偶数,则需要保证两数都是偶数),如果找到g*2^k,则跳到步骤六。
五、在步骤四的循环中选择含有数被4整除得奇数(且该数减半小于x)的数组(如果x是偶数则选择被2整除的),将该数偶变换给0,再重新在两数之间不断进行偶变换(如果x是偶数,则需要保证两数都是偶数),出现g*2^k则结束,将另两个数合并。
六、用二进制数表示x/g,在左边补充0直到位数等于k,从最高位到最低位,若为1则将g*2^k分配给0(或者是步骤五中得到g*2^k一半的数),为0则分配给另一个数。这样就得到了x,结束。
虽然有很多漏洞,但大框架是对的。在下文逐步分析后,我们将会推导出一个正确的通解。
直接得到通解可能是困难的,于是我想着要不然先解决什么样的组合是可解的问题吧。反复观察变换路径后,我猜测g整除x应该和有解相关,并且还发现了og在变换的过程中不变或变大,而且变换后的og整除变换前的og。
然后,我再想的是解决相对简单的数组。在三个数之间变换是复杂的,暂未发现规律,所以我研究了只有一个数为0的数组。如果三个正数的数组都能转变为一零两正,那么通解问题就可以归约到一零两正如何变换出x或2x的问题。
我们需要保证三正变两正后,g依然满足g|x。如何操作呢?对于{a,b,c},奇变换后得到的{0,a+b,c}, {0,b,a+c}和{a,0,b+c}三个数组中,一定有一个数组的g满足g|x。
证明:3x的质因数分解为m*3^n,(m,n)=1。先假设三个数组的g都不整除x。(a+b,c)=(3x,c),(a+c,b)=(3x,b),(b+c,a)=(3x,a)如果都不整除x,则(3^n)|(a,b,c),又因为(a,b,c)|x,可得(3^n)|x,但3x=m*3^n,(m,3)=1,矛盾。
两奇一偶时(该偶数不为0),以上的三种操作可能会让数组变为一零两奇,因此我们要对该类情况作调整,它有两种变换:一、两奇相加;二、偶数拆分为两奇数,分别加给另外两奇数。这两种变换会使三正变一零两偶,且至少有一种使得g|x,证明类似上一个,不再赘述。这样的话,我们就将前面提到的可解的数组都转化为一零两正了。
前面说过{0,0,3x}是无解的,两个正数不能奇变换,那当然就只好偶变换了。当x为奇数时,两个数一奇一偶,偶变换的对象(即哪个数给另一个数一半)是确定的,得到的下一数组是唯一的。再加上数组的和是不变的,这样的数组个数有限,所以,经过有限次偶变换后,一定会回到原来的数组,形成偶变换循环。当x为偶数时,偶变换的路径是不唯一的,且不一定能不断偶变换,变换后还可能是一零两奇,比如{2,10}。x为偶数的这种情况,后续在改进偶变换的时候再提及。
我们的目标是在循环中找到t*2^k,t*2^k>=x,t|x,k>0,因为在有三个数时,将t*2^k偶变换分解,可以得到小于t*2^k任意一个自然数。但循环中并不一定有t*2^k(比如{5,28}),所以在早期的想法中,我想打破原有循环,把偶数偶变换分给第三个数,使得原来循环的两个数进入新的循环,以找到t*2^k。
在{a,b}的偶变换循环中,如果我们只关注其中一个数a,可以发现该数在作如下变换:偶数时减半,奇数时加上sum再减半,sum=a+b。冰雹猜想里的变换会迭代至2^k,而这里,迭代至t*2^k,a和sum要满足的所有条件是什么,是个open的问题。修改了几次进入新循环的方法后,程序依然发现反例。所以,探寻如何修正a和sum进入新的含有t*2^k的循环,这条路暂时行不通。
不小于x的t*2^k一定和小于x的t*2^k在同一循环中,找到其中一个便能找到其余的t*2^k。但要得到新的循环,就要将参与偶变换循环的两数之和sum减小,而最大的t*2^k满足t*2^k
这样我们就有一个新的思路,先找到小于x的t*2k,再保持t*2^k不变,将sum增大使得sum>2x,进行新一轮偶变换,得到不小于x的t*2^k。
在偶变换时,如果偶数减半后还是偶数,则将这一部分加到第三个数上,这样我们就将前面总和不变的循环改成了总和递减的。由于无论怎么变换三个数都必为自然数,循环的总和不能无限递减,那它的下界是多少呢?当不能再分配给第三个数时,总和不变,因此偶变换一次,对象就交换,此后的所有偶数除以2后都为奇数,假设(a,b)中a为偶数,此时偶数a的变换如下:
a
a/2
a/4+sum
a/8+sum/2
a/16+sum/4+sum
a/32+sum/8+sum/2
a/64+sum/16+sum/4+sum
...
第n个偶数和第n-1偶数的递推式为x_n+1=x_n/4+sum,x_0=a
可得通式x_n=(a-4sum/3)/4^n+4sum/3
当a>4sum/3时,x_n单调递增,当a<4sum/3时,x_n单调递减,数组的大小是有限的,不能单调递增或递减,因此a=4sum/3=2a/3+2b/3,可得a=2b,偶变换循环的过程中,a和b的最大奇公约数og始终不变,又因为b是奇数,b和2b的最大奇公约数为b,所以,当sum最小时,a=2b=2og。前面的三正变两正保持了g|x,所以b|x。
当x为奇数时,将{b,2b,3x-3b}转化为{b,3x-2b,0},再对两正数偶变换即可得到t*2^k<=3x<=t*2^(k+1),此时的t*2^k>=3x/2>x,可进行二进制分配。不过,我们不必操作至sum递减至3b,如果过程中出现了t*2^k,若其不小于x自然不用说,若小于x,则将另两个数合并再偶变换就能得到不小于x的。
当x为偶数时,3x-3b为奇数,如果a>=x,则a二进制分配即可得x,如果a
t*2^k>=(3x-b)/2>=5x/4>x。同样地,我们不一定要等sum减到3b,出现小于x的t*2^k时,t*2^k一定是循环中最大的,大于与它偶变换的奇数u,设第三个数为v,v是奇数,则由t*2^k
综上,我们得到了一个通解:
一、有x或2x则结束。
二、数组中是否有q=t*2^k,其中t|x,且q>x,k>0(第一次找到q或者q>x,需要将另两数合并),是则将q以外的另两个数合并,跳至六
三、是否q
四、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择其中g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分成奇数给两奇数,选择其中g整除x的数组。
五、进行步骤一二三,若偶变换的数不是偶数,则交换对象,一个偶数减半后,若参与偶变换的两个数不都是奇数,则不断进行偶变换,否则分配给第三个数(如果已经找到q则永远不再分配给第三个数),继续五。
六、用二进制数表示x/t,在左边补充0直到位数等于k,从最高位到最低位,若为1则将q分配给0,为0则分配给另一个数。这样就得到了x,结束。
至此,我们从理论上推导证明了通解的可行性,此外,我还写了验证该解法的cpp代码,对0<=x<=1000的所有有解数组都进行了验证并且验证成功。
当然,也许还存在其他通解,我很期待看到新想法。
我爱解压好玩吗 我爱解压玩法简介
期待已久的手游我爱解压即将登陆九游,这款手机游戏吸引了大批玩家的关注,想下载这款游戏,有很多粉丝都在问九游小编我爱解压好玩吗?我爱解压值不值得玩?现在就为大家来简单分析下,看看这款游戏的玩法特点和游戏剧情介绍 。
我爱解压快速预约/下载地址(需优先下载九游APP):
》》》》》#我爱解压#《《《《《
1、我爱解压简要评析:
欢迎游玩《我爱解压》,这是一款极致的清洁游戏体验,干净整洁是成功的关键!在这里,你将踏上一段建立和扩展自己餐厅的旅程,探索餐厅管理的世界。 清理凌乱的房间,清除垃圾,为你梦想中的餐厅奠定基础。随着你的进展,解锁收银机、食品摊位和餐桌,吸引顾客并增加你的收入。 但成功不仅仅是赚钱 —— 保持清洁整洁同样至关重要。雇佣服务员保持桌面整洁,确保顾客享受愉快的就餐体验。及时清理垃圾,保持店面清洁,让顾客满意。清洁是保持生意持续的关键 —— 对地板进行高压清洗,清理沙滩,过上整洁的生活! 随着利润的增长,你的餐厅也会不断扩展。解锁新的房间,扩展你的商业帝国,升级你的角色和服务员,增加能力和效率,看着你的利润飙升。在清洁游戏的世界里,《我爱解压》为你带来独特的清洁和业务管理体验! 游戏特点: 餐厅扩展:清理新房间,获得更多现金和顾客! 升级你的业务:摆放餐桌,开设酒吧,提供美食! 雇佣员工:聘请清洁工,保持一切整洁 —— 确保你升级他们以提高清洁能力! 凭借着令人上瘾的游戏玩法、迷人的图形和无限扩展的可能性,《我爱解压》为所有喜欢经营游戏的玩家提供了数小时的娱乐。你准备好卷起袖子,清理和打造你梦想中的餐厅了吗?立即下载《我爱解压》,让清洁游戏的狂潮开始吧!
2、我爱解压图片欣赏:
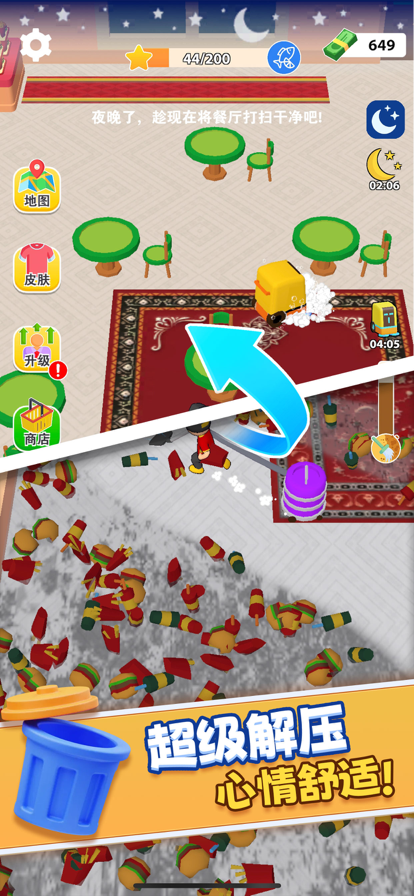
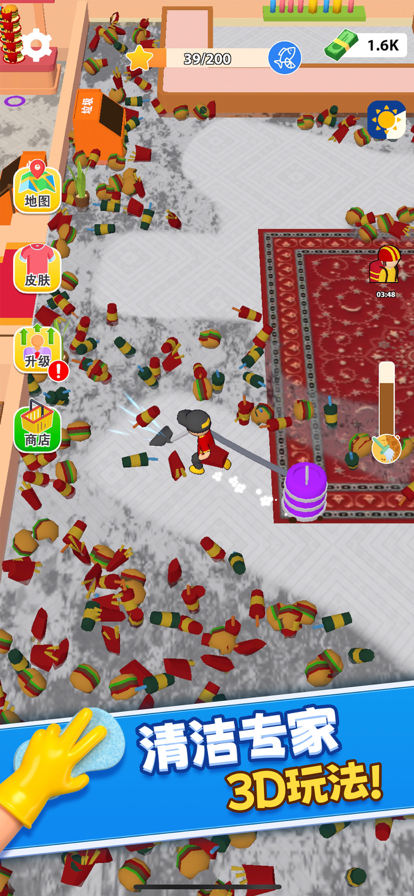

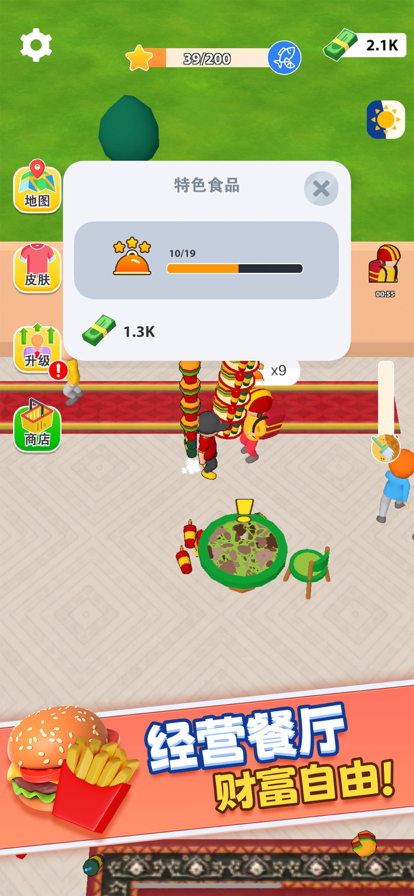
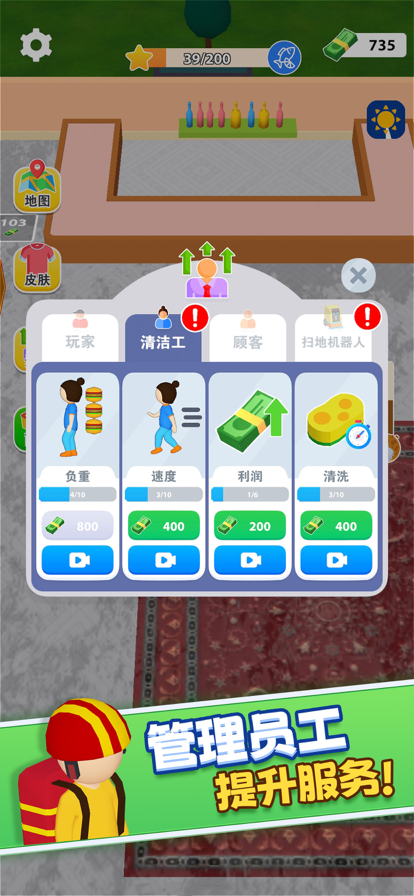
通过上面的游戏介绍和图片,可能大家对我爱解压有大致的了解了,不过这么游戏要怎么样才能抢先体验到呢?不用担心,目前九游客户端已经开通了测试提醒了,通过在九游APP中搜索“我爱解压”,点击右边的【订阅】或者是【开测提醒】,订阅游戏就不会错过最先的下载机会了咯!
 全球好游抢先下
全球好游抢先下 福利礼包免费领
福利礼包免费领 官方直播陪你玩
官方直播陪你玩
我数学特强小游戏怎么玩
我数学特强小游戏怎么玩?近期这款游戏人气真的是非常火爆,游戏的关卡挑战很多,但是只要玩家掌握了其中的技巧,那么就能很快完成全部关卡的挑战,接下来九游小编就给大家带来了我数学特强全关卡通关技巧分享,希望能帮助到大家,一起来看看吧。
我数学特强全关卡通关技巧分享

我数学特强小游戏攻略
最后一步是3X,倒数第二步一定是2X+X(限1),倒数第三步一定是两个相加等于2X的数+X(限2)或者两个相加等于X的数+2X。
所以核心关键就是凑2X。
两个一样的数字不要合成,没意义。
看到所有的偶数都要第一时间在脑子里拆成奇数,和剩余的奇数去配X。
因为都是两两合成,所以记住这两个关键数:
1、2、4、8、16。
3、6、12、24。
1系列能拆出:
4和12,6和10,5和11,
以及
4和12,2和14,7和9(或1和15)。
3系列能拆出:
6和18,3和21,
以及
6和18,9和15。
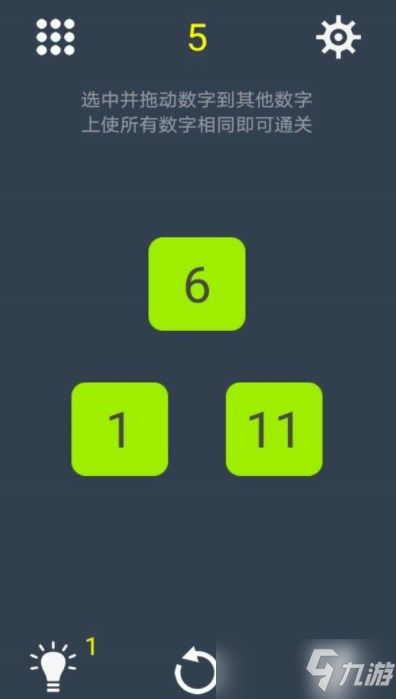
在倒数第二步先凑出总数的三分之一或者三分之二,这样就可以少考虑两步更简单点。
偷鸡小技巧:
总和除以3就是目标数字
凑出8或者16 这关基本上就过了
8可以变成1~7 16可以变成两个8 其中一个8变成1 可以获得9 得到目标数字剩下对半拆
(所以我一直以8或16为目标过了前80关……)
经常会遇到5 12 7的情况 把12拆两次给7 得到16 游戏结束……
大家可以看看这篇文章,九游小编给大家带来的我数学特强全关卡通关技巧分享,请关注九游手游网以获取第一时间的资讯更新信息。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
我爱玩手好玩吗 我爱玩手玩法简介
期待已久的手游我爱玩手即将登陆九游,这款手机游戏吸引了大批玩家的关注,有很多粉丝都在问九游小编我爱玩手好玩吗?我爱玩手值不值得玩?现在就为大家来简单分析下,看看这款游戏的玩法特点和游戏剧情介绍。
1、我爱玩手简要评析:
我爱玩手是一款非常不错的休闲益智类游戏,这款游戏的玩法非常的简单,你将通过手指的动作来与关卡的形状相对应才可完成挑战,非常考验你的肢体协调能力,是一款非常适合打发无聊时间的趣味游戏,感兴趣的话请点击链接进行下载吧!
2、我爱玩手图片欣赏:



通过上面的游戏介绍和图片,可能大家对我爱玩手有大致的了解了,不过这么游戏要怎么样才能抢先体验到呢?不用担心,目前九游客户端已经开通了测试提醒了,通过在九游APP中搜索“我爱玩手”,点击右边的【订阅】或者是【开测提醒】,订阅游戏就不会错过最先的下载机会了咯!
 全球好游抢先下
全球好游抢先下 福利礼包免费领
福利礼包免费领 官方直播陪你玩
官方直播陪你玩
数学游戏 我爱数学
「我爱数学:MathMathMath」是一款寓教于乐的数学类游戏,画风比较学院,非常适合小朋友玩,在玩游戏的过程中不知不觉学习数学知识,我爱数学,数学使我快乐~
九游括三种模式:
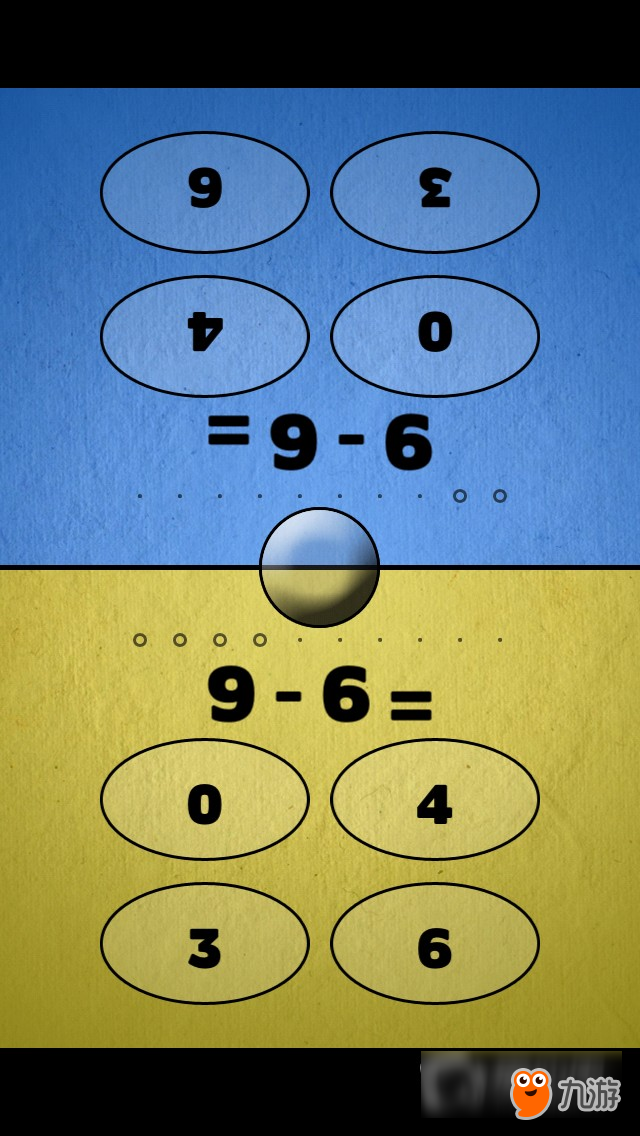
多人游戏:在同一个iPad或者手机上尽快点击正确的答案并收集积分,第一个拿到10分的赢得比赛。
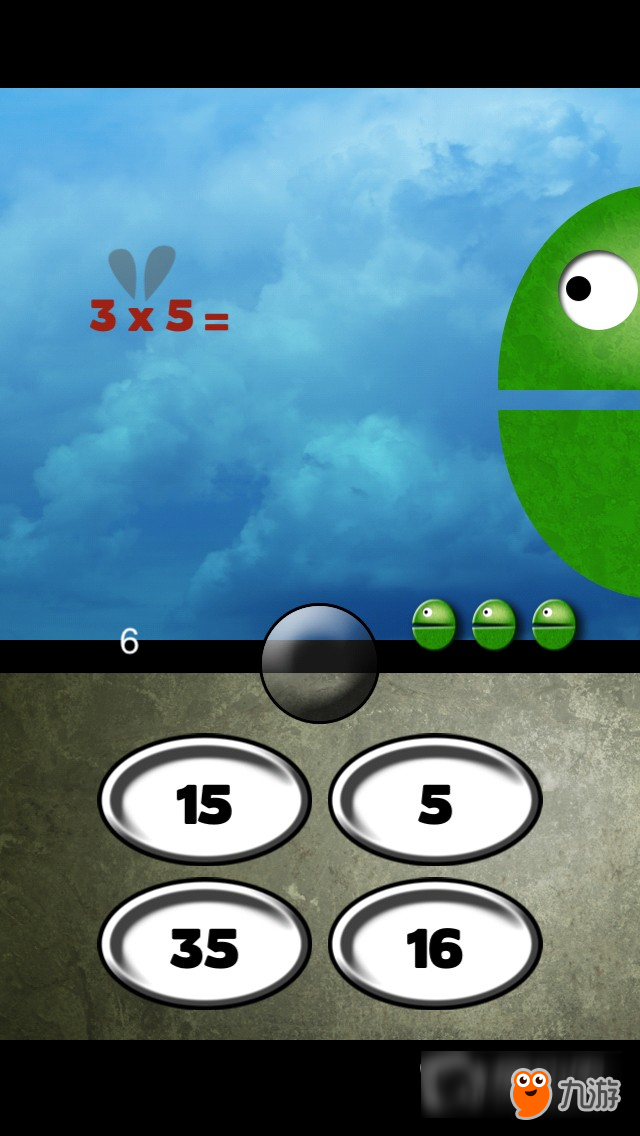
青蛙游戏(单人游戏):点击正确的答案则青蛙就能吃到食物,否则就会失败。
相机游戏(单人游戏):- 同时改善你的健身和你的精神数学技能!游戏可以直接从相机图像中检测出你的动作!在相机前移动,并在空中触摸正确的答案。使用iPad智能外盖将iPad放在直立位置,然后在相机前方跳动,或将设备平放在桌子上,并将其中一根手指移动到相机前方。注意:仅适用于具有正面(面对面)相机的设备(iPad第2代和更新版,iPod第4代及更高版本)。

难得一见的寓教于乐的数学游戏,赶紧下载起来吧~

我爱数学同类推荐
相关专题
最新专题
- 耐玩的acg游戏下载推荐
- 受欢迎的网易手游有哪些
- 流行的免费数独游戏有哪些
- 有意思的五人游戏大全
- 雄心之上在哪里下载
- 受欢迎的诸神游戏哪里下载
- 受欢迎的消除小游戏盘点
- 有趣的跑跑手游有哪几个
- 有没有耐玩的无限游戏
- 网吧游戏热度排行榜分享
- 流行的少女养成游戏下载
- 星布谷地手游下载地址分享
- 有趣的拆弹专家游戏手机版下载
- 舞力全开派对去哪里下载
- 有趣的枪战游戏下载推荐
- 斗破苍穹手游下载地址
- 机械启元免费下载地址分享
- 星布谷地安卓版下载地址分享
- 代号足球下载渠道在哪儿
- 耐玩的同屏双人游戏有哪些
- 代号足球预约方法是什么
- 射击小游戏单机游戏叫什么
- 耐玩的升一级三选一技能的游戏推荐
- 训练专注力的小游戏大全
- 刺激的拉力赛游戏手机版有哪些
- 受欢迎的外服游戏有没有
- 好玩的二次元手游有哪些
- 耐玩的改装车游戏推荐
- 火爆的游戏王系列手游有没有
- 有哪些地铁逃生的游戏
游戏排行


即将上线










最新游戏
最新资讯

















































 粤公网安备44010602000283号
粤公网安备44010602000283号
