刺骨的数学

我数学特强《我数学特强》通解是存在的！如下：

《我数学特强》有没有万能公式呢？很久之前，一开始玩的时候，就想过这个问题，但面对复杂的变换路径，我完全没有头绪。

最近的研究让我找到了通用的解法，这不是用程序暴力搜索答案，也不是简要的技巧，而是公式化的解法。另外，游戏里要求使用最少步数的最优解，而通解一般不限步数。

介绍一下游戏。有三个自然数，玩家每次操作可以对这三个数进行分配，我称为偶变换和奇变换，偶变换是把一个偶数减半并将减半的部分加到另一个数上，奇变换是把一个奇数加到另一个数上，然后将其变为0。实际上，奇变换不限奇数，因为将偶数奇变换给另一个数，可以先一直偶变换直到变为奇数，再进行奇变换。游戏的最终目标是得到三个相等的数，用三元数组表示为{x, x, x}，不过显然只要三个数里有x或2x就能得到{x, x, x}。

有通解的前提是有解，而有解的充要条件是，三个数的最大公约数g整除x（可表示为g|x），且三个数不是一零二奇。先证明必要性，og和og'分别为三个数变换前后的最大奇公约数，易证og|og'，如果og'=x，则og|x，也就是说如果得到了{x,x,x}，则有og|x，因此og|x是有解的必要条件。另外，由g=(a,b,c)（三个数a,b,c的最大公约数写法为(a,b,c)），可得g|3x，令g=og*2^m，则(og*2^m)|3x，(2^m)|(3x/og)，而(2^m,3)=1，所以(2^m)|(x/og)，(og*2^m)|x，可得g|x也是有解的必要条件，其逆否命题为，若g不整除x，则无解，而(0,0,3x)不整除x，一零两奇时只能奇变换为{0,0,3x}，两者等价，所以三数不是一零两奇也是有解的必要条件。至于充分性，如果我们找到了g|x且不是一零两奇情况下的解法，就相当于将其证明了。

通解讨论的数组默认已通过以上判别法筛选，以保证有解及证明充分性。但要注意，有解的数组在变换后不一定有解，通解的操作应当保证数组在变换后依然可解，时刻有g|x。

下面的是我早期想的通解，经过计算机验证，x为奇数时，x>17后出现反例：

一、有x或2x则结束。

三、若三数都是正数，且不是两奇一偶，则尝试将其中一个数加给另外两个数中的一个数，选择三种操作进行后g整除x的数组；若三数都是正数，且两奇一偶，则将两奇数相加，或将偶数分配给两奇数使其变为两偶数，选择两种操作进行后g整除x的数组。

四、若数组中没有g*2^k满足g*2^k>=x，k是自然数，则不断在两正数之间进行偶变换（如果x是偶数，则需要保证两数都是偶数），如果找到g*2^k，则跳到步骤六。

五、在步骤四的循环中选择含有数被4整除得奇数（且该数减半小于x）的数组（如果x是偶数则选择被2整除的），将该数偶变换给0，再重新在两数之间不断进行偶变换（如果x是偶数，则需要保证两数都是偶数），出现g*2^k则结束，将另两个数合并。

六、用二进制数表示x/g，在左边补充0直到位数等于k，从最高位到最低位，若为1则将g*2^k分配给0（或者是步骤五中得到g*2^k一半的数），为0则分配给另一个数。这样就得到了x，结束。

虽然有很多漏洞，但大框架是对的。在下文逐步分析后，我们将会推导出一个正确的通解。

直接得到通解可能是困难的，于是我想着要不然先解决什么样的组合是可解的问题吧。反复观察变换路径后，我猜测g整除x应该和有解相关，并且还发现了og在变换的过程中不变或变大，而且变换后的og整除变换前的og。

然后，我再想的是解决相对简单的数组。在三个数之间变换是复杂的，暂未发现规律，所以我研究了只有一个数为0的数组。如果三个正数的数组都能转变为一零两正，那么通解问题就可以归约到一零两正如何变换出x或2x的问题。

我们需要保证三正变两正后，g依然满足g|x。如何操作呢？对于{a,b,c}，奇变换后得到的{0,a+b,c}, {0,b,a+c}和{a,0,b+c}三个数组中，一定有一个数组的g满足g|x。

证明：3x的质因数分解为m*3^n，(m,n)=1。先假设三个数组的g都不整除x。(a+b,c)=(3x,c)，(a+c,b)=(3x,b)，(b+c,a)=(3x,a)如果都不整除x，则(3^n)|(a,b,c)，又因为(a,b,c)|x，可得(3^n)|x，但3x=m*3^n，(m,3)=1，矛盾。

两奇一偶时（该偶数不为0），以上的三种操作可能会让数组变为一零两奇，因此我们要对该类情况作调整，它有两种变换：一、两奇相加；二、偶数拆分为两奇数，分别加给另外两奇数。这两种变换会使三正变一零两偶，且至少有一种使得g|x，证明类似上一个，不再赘述。这样的话，我们就将前面提到的可解的数组都转化为一零两正了。

前面说过{0,0,3x}是无解的，两个正数不能奇变换，那当然就只好偶变换了。当x为奇数时，两个数一奇一偶，偶变换的对象（即哪个数给另一个数一半）是确定的，得到的下一数组是唯一的。再加上数组的和是不变的，这样的数组个数有限，所以，经过有限次偶变换后，一定会回到原来的数组，形成偶变换循环。当x为偶数时，偶变换的路径是不唯一的，且不一定能不断偶变换，变换后还可能是一零两奇，比如{2,10}。x为偶数的这种情况，后续在改进偶变换的时候再提及。

我们的目标是在循环中找到t*2^k，t*2^k>=x，t|x，k>0，因为在有三个数时，将t*2^k偶变换分解，可以得到小于t*2^k任意一个自然数。但循环中并不一定有t*2^k（比如{5,28}），所以在早期的想法中，我想打破原有循环，把偶数偶变换分给第三个数，使得原来循环的两个数进入新的循环，以找到t*2^k。

在{a,b}的偶变换循环中，如果我们只关注其中一个数a，可以发现该数在作如下变换：偶数时减半，奇数时加上sum再减半，sum=a+b。冰雹猜想里的变换会迭代至2^k，而这里，迭代至t*2^k，a和sum要满足的所有条件是什么，是个open的问题。修改了几次进入新循环的方法后，程序依然发现反例。所以，探寻如何修正a和sum进入新的含有t*2^k的循环，这条路暂时行不通。

不小于x的t*2^k一定和小于x的t*2^k在同一循环中，找到其中一个便能找到其余的t*2^k。但要得到新的循环，就要将参与偶变换循环的两数之和sum减小，而最大的t*2^k满足t*2^k sum/2。

这样我们就有一个新的思路，先找到小于x的t*2k，再保持t*2^k不变，将sum增大使得sum>2x，进行新一轮偶变换，得到不小于x的t*2^k。

在偶变换时，如果偶数减半后还是偶数，则将这一部分加到第三个数上，这样我们就将前面总和不变的循环改成了总和递减的。由于无论怎么变换三个数都必为自然数，循环的总和不能无限递减，那它的下界是多少呢？当不能再分配给第三个数时，总和不变，因此偶变换一次，对象就交换，此后的所有偶数除以2后都为奇数，假设(a,b)中a为偶数，此时偶数a的变换如下：

a

a/2

a/4+sum

a/8+sum/2

a/16+sum/4+sum

a/32+sum/8+sum/2

a/64+sum/16+sum/4+sum

...

第n个偶数和第n-1偶数的递推式为x_n+1=x_n/4+sum，x_0=a

可得通式x_n=(a-4sum/3)/4^n+4sum/3

当a>4sum/3时，x_n单调递增，当a<4sum/3时，x_n单调递减，数组的大小是有限的，不能单调递增或递减，因此a=4sum/3=2a/3+2b/3，可得a=2b，偶变换循环的过程中，a和b的最大奇公约数og始终不变，又因为b是奇数，b和2b的最大奇公约数为b，所以，当sum最小时，a=2b=2og。前面的三正变两正保持了g|x，所以b|x。

当x为奇数时，将{b,2b,3x-3b}转化为{b,3x-2b,0}，再对两正数偶变换即可得到t*2^k<=3x<=t*2^(k+1)，此时的t*2^k>=3x/2>x，可进行二进制分配。不过，我们不必操作至sum递减至3b，如果过程中出现了t*2^k，若其不小于x自然不用说，若小于x，则将另两个数合并再偶变换就能得到不小于x的。

当x为偶数时，3x-3b为奇数，如果a>=x，则a二进制分配即可得x，如果a 3x/2>b，让a和3x-3b偶变换得到新的t*2^k，满足t*2^k<=3x-b<=t*2^(k+1)，于是

t*2^k>=(3x-b)/2>=5x/4>x。同样地，我们不一定要等sum减到3b，出现小于x的t*2^k时，t*2^k一定是循环中最大的，大于与它偶变换的奇数u，设第三个数为v，v是奇数，则由t*2^k x，让t*2^k和v偶变换得到的新的最大的t*2^k满足t*2^k>=(t*2^k+v)/2=(3x-u)/2>x。这样一来，即使t*2^k

综上，我们得到了一个通解：

一、有x或2x则结束。

二、数组中是否有q=t*2^k，其中t|x，且q>x，k>0（第一次找到q或者q>x，需要将另两数合并），是则将q以外的另两个数合并，跳至六

三、是否q

四、若三数都是正数，且不是两奇一偶，则尝试将其中一个数加给另外两个数中的一个数，选择其中g整除x的数组；若三数都是正数，且两奇一偶，则将两奇数相加，或将偶数分成奇数给两奇数，选择其中g整除x的数组。

五、进行步骤一二三，若偶变换的数不是偶数，则交换对象，一个偶数减半后，若参与偶变换的两个数不都是奇数，则不断进行偶变换，否则分配给第三个数（如果已经找到q则永远不再分配给第三个数），继续五。

六、用二进制数表示x/t，在左边补充0直到位数等于k，从最高位到最低位，若为1则将q分配给0，为0则分配给另一个数。这样就得到了x，结束。

至此，我们从理论上推导证明了通解的可行性，此外，我还写了验证该解法的cpp代码，对0<=x<=1000的所有有解数组都进行了验证并且验证成功。

当然，也许还存在其他通解，我很期待看到新想法。

我数学特强《我数学特强》通解是存在的！如下：

《我数学特强》有没有万能公式呢？很久之前，一开始玩的时候，就想过这个问题，但面对复杂的变换路径，我完全没有头绪。

最近的研究让我找到了通用的解法，这不是用程序暴力搜索答案，也不是简要的技巧，而是公式化的解法。另外，游戏里要求使用最少步数的最优解，而通解一般不限步数。

介绍一下游戏。有三个自然数，玩家每次操作可以对这三个数进行分配，我称为偶变换和奇变换，偶变换是把一个偶数减半并将减半的部分加到另一个数上，奇变换是把一个奇数加到另一个数上，然后将其变为0。实际上，奇变换不限奇数，因为将偶数奇变换给另一个数，可以先一直偶变换直到变为奇数，再进行奇变换。游戏的最终目标是得到三个相等的数，用三元数组表示为{x, x, x}，不过显然只要三个数里有x或2x就能得到{x, x, x}。

有通解的前提是有解，而有解的充要条件是，三个数的最大公约数g整除x（可表示为g|x），且三个数不是一零二奇。先证明必要性，og和og'分别为三个数变换前后的最大奇公约数，易证og|og'，如果og'=x，则og|x，也就是说如果得到了{x,x,x}，则有og|x，因此og|x是有解的必要条件。另外，由g=(a,b,c)（三个数a,b,c的最大公约数写法为(a,b,c)），可得g|3x，令g=og*2^m，则(og*2^m)|3x，(2^m)|(3x/og)，而(2^m,3)=1，所以(2^m)|(x/og)，(og*2^m)|x，可得g|x也是有解的必要条件，其逆否命题为，若g不整除x，则无解，而(0,0,3x)不整除x，一零两奇时只能奇变换为{0,0,3x}，两者等价，所以三数不是一零两奇也是有解的必要条件。至于充分性，如果我们找到了g|x且不是一零两奇情况下的解法，就相当于将其证明了。

通解讨论的数组默认已通过以上判别法筛选，以保证有解及证明充分性。但要注意，有解的数组在变换后不一定有解，通解的操作应当保证数组在变换后依然可解，时刻有g|x。

下面的是我早期想的通解，经过计算机验证，x为奇数时，x>17后出现反例：

一、有x或2x则结束。

三、若三数都是正数，且不是两奇一偶，则尝试将其中一个数加给另外两个数中的一个数，选择三种操作进行后g整除x的数组；若三数都是正数，且两奇一偶，则将两奇数相加，或将偶数分配给两奇数使其变为两偶数，选择两种操作进行后g整除x的数组。

四、若数组中没有g*2^k满足g*2^k>=x，k是自然数，则不断在两正数之间进行偶变换（如果x是偶数，则需要保证两数都是偶数），如果找到g*2^k，则跳到步骤六。

五、在步骤四的循环中选择含有数被4整除得奇数（且该数减半小于x）的数组（如果x是偶数则选择被2整除的），将该数偶变换给0，再重新在两数之间不断进行偶变换（如果x是偶数，则需要保证两数都是偶数），出现g*2^k则结束，将另两个数合并。

六、用二进制数表示x/g，在左边补充0直到位数等于k，从最高位到最低位，若为1则将g*2^k分配给0（或者是步骤五中得到g*2^k一半的数），为0则分配给另一个数。这样就得到了x，结束。

虽然有很多漏洞，但大框架是对的。在下文逐步分析后，我们将会推导出一个正确的通解。

直接得到通解可能是困难的，于是我想着要不然先解决什么样的组合是可解的问题吧。反复观察变换路径后，我猜测g整除x应该和有解相关，并且还发现了og在变换的过程中不变或变大，而且变换后的og整除变换前的og。

然后，我再想的是解决相对简单的数组。在三个数之间变换是复杂的，暂未发现规律，所以我研究了只有一个数为0的数组。如果三个正数的数组都能转变为一零两正，那么通解问题就可以归约到一零两正如何变换出x或2x的问题。

我们需要保证三正变两正后，g依然满足g|x。如何操作呢？对于{a,b,c}，奇变换后得到的{0,a+b,c}, {0,b,a+c}和{a,0,b+c}三个数组中，一定有一个数组的g满足g|x。

证明：3x的质因数分解为m*3^n，(m,n)=1。先假设三个数组的g都不整除x。(a+b,c)=(3x,c)，(a+c,b)=(3x,b)，(b+c,a)=(3x,a)如果都不整除x，则(3^n)|(a,b,c)，又因为(a,b,c)|x，可得(3^n)|x，但3x=m*3^n，(m,3)=1，矛盾。

两奇一偶时（该偶数不为0），以上的三种操作可能会让数组变为一零两奇，因此我们要对该类情况作调整，它有两种变换：一、两奇相加；二、偶数拆分为两奇数，分别加给另外两奇数。这两种变换会使三正变一零两偶，且至少有一种使得g|x，证明类似上一个，不再赘述。这样的话，我们就将前面提到的可解的数组都转化为一零两正了。

前面说过{0,0,3x}是无解的，两个正数不能奇变换，那当然就只好偶变换了。当x为奇数时，两个数一奇一偶，偶变换的对象（即哪个数给另一个数一半）是确定的，得到的下一数组是唯一的。再加上数组的和是不变的，这样的数组个数有限，所以，经过有限次偶变换后，一定会回到原来的数组，形成偶变换循环。当x为偶数时，偶变换的路径是不唯一的，且不一定能不断偶变换，变换后还可能是一零两奇，比如{2,10}。x为偶数的这种情况，后续在改进偶变换的时候再提及。

我们的目标是在循环中找到t*2^k，t*2^k>=x，t|x，k>0，因为在有三个数时，将t*2^k偶变换分解，可以得到小于t*2^k任意一个自然数。但循环中并不一定有t*2^k（比如{5,28}），所以在早期的想法中，我想打破原有循环，把偶数偶变换分给第三个数，使得原来循环的两个数进入新的循环，以找到t*2^k。

在{a,b}的偶变换循环中，如果我们只关注其中一个数a，可以发现该数在作如下变换：偶数时减半，奇数时加上sum再减半，sum=a+b。冰雹猜想里的变换会迭代至2^k，而这里，迭代至t*2^k，a和sum要满足的所有条件是什么，是个open的问题。修改了几次进入新循环的方法后，程序依然发现反例。所以，探寻如何修正a和sum进入新的含有t*2^k的循环，这条路暂时行不通。

不小于x的t*2^k一定和小于x的t*2^k在同一循环中，找到其中一个便能找到其余的t*2^k。但要得到新的循环，就要将参与偶变换循环的两数之和sum减小，而最大的t*2^k满足t*2^k sum/2。

这样我们就有一个新的思路，先找到小于x的t*2k，再保持t*2^k不变，将sum增大使得sum>2x，进行新一轮偶变换，得到不小于x的t*2^k。

在偶变换时，如果偶数减半后还是偶数，则将这一部分加到第三个数上，这样我们就将前面总和不变的循环改成了总和递减的。由于无论怎么变换三个数都必为自然数，循环的总和不能无限递减，那它的下界是多少呢？当不能再分配给第三个数时，总和不变，因此偶变换一次，对象就交换，此后的所有偶数除以2后都为奇数，假设(a,b)中a为偶数，此时偶数a的变换如下：

a

a/2

a/4+sum

a/8+sum/2

a/16+sum/4+sum

a/32+sum/8+sum/2

a/64+sum/16+sum/4+sum

...

第n个偶数和第n-1偶数的递推式为x_n+1=x_n/4+sum，x_0=a

可得通式x_n=(a-4sum/3)/4^n+4sum/3

当a>4sum/3时，x_n单调递增，当a<4sum/3时，x_n单调递减，数组的大小是有限的，不能单调递增或递减，因此a=4sum/3=2a/3+2b/3，可得a=2b，偶变换循环的过程中，a和b的最大奇公约数og始终不变，又因为b是奇数，b和2b的最大奇公约数为b，所以，当sum最小时，a=2b=2og。前面的三正变两正保持了g|x，所以b|x。

当x为奇数时，将{b,2b,3x-3b}转化为{b,3x-2b,0}，再对两正数偶变换即可得到t*2^k<=3x<=t*2^(k+1)，此时的t*2^k>=3x/2>x，可进行二进制分配。不过，我们不必操作至sum递减至3b，如果过程中出现了t*2^k，若其不小于x自然不用说，若小于x，则将另两个数合并再偶变换就能得到不小于x的。

当x为偶数时，3x-3b为奇数，如果a>=x，则a二进制分配即可得x，如果a 3x/2>b，让a和3x-3b偶变换得到新的t*2^k，满足t*2^k<=3x-b<=t*2^(k+1)，于是

t*2^k>=(3x-b)/2>=5x/4>x。同样地，我们不一定要等sum减到3b，出现小于x的t*2^k时，t*2^k一定是循环中最大的，大于与它偶变换的奇数u，设第三个数为v，v是奇数，则由t*2^k x，让t*2^k和v偶变换得到的新的最大的t*2^k满足t*2^k>=(t*2^k+v)/2=(3x-u)/2>x。这样一来，即使t*2^k

综上，我们得到了一个通解：

一、有x或2x则结束。

二、数组中是否有q=t*2^k，其中t|x，且q>x，k>0（第一次找到q或者q>x，需要将另两数合并），是则将q以外的另两个数合并，跳至六

三、是否q

四、若三数都是正数，且不是两奇一偶，则尝试将其中一个数加给另外两个数中的一个数，选择其中g整除x的数组；若三数都是正数，且两奇一偶，则将两奇数相加，或将偶数分成奇数给两奇数，选择其中g整除x的数组。

五、进行步骤一二三，若偶变换的数不是偶数，则交换对象，一个偶数减半后，若参与偶变换的两个数不都是奇数，则不断进行偶变换，否则分配给第三个数（如果已经找到q则永远不再分配给第三个数），继续五。

六、用二进制数表示x/t，在左边补充0直到位数等于k，从最高位到最低位，若为1则将q分配给0，为0则分配给另一个数。这样就得到了x，结束。

至此，我们从理论上推导证明了通解的可行性，此外，我还写了验证该解法的cpp代码，对0<=x<=1000的所有有解数组都进行了验证并且验证成功。

当然，也许还存在其他通解，我很期待看到新想法。

在dnf（地下城与勇士）这个游戏世界里，武器是非常关键的一个环节。特别是对于输出职业，武器的选择直接影响着战斗的胜败。今天我们就来讨论一种备受玩家关注的武器——刺骨。

二、全文分析

（一）武器介绍

刺骨是一种非常独特的刺剑，其属性加成和特效在游戏中独树一帜。它属于魔法攻击，物理攻击和魔法攻击均有效果，同时附加出血和感电效果，使得它在许多战斗中都能发挥出强大的威力。刺骨的属性加成对于鬼剑士、格斗家等职业来说是非常适合的。在游戏早期，刺骨的获取难度相对较高，但随着游戏的推进，它的价值也逐渐显现出来。

（二）武器选择

1. 刺骨的优势：特效强大，伤害可观；出血和感电效果有助于快速击败敌人；附加属性较多，适合多种职业。

2. 刺骨的劣势：获取难度较高，需要花费较多时间和金钱；对操作要求较高，新手玩家可能不太适应。在选择使用刺骨时，玩家需要根据自己的实际情况进行权衡。一般来说，对于有一定操作基础，并且愿意投入时间和金钱的玩家，使用刺骨是一种非常不错的选择。而对于新手玩家或者不愿意投入太多资源的玩家，选择其他类型的武器可能更为合适。

（三）实战应用

刺骨作为一种魔法攻击武器，非常适合依赖普通攻击的职业如鬼剑士和格斗家。同时，其特效也使其在战斗中能够迅速击败敌人并形成连击。具体应用时，玩家需要根据实际情况选择合适的技能和战术，例如利用出血和感电效果提高伤害，或者通过技能连击快速击败敌人。在组队战斗中，刺骨的特效也能够帮助队友快速击败敌人，提高整体战斗效率。

（四）总结和建议

总的来说，刺骨是一种非常强大的武器，但它的获取难度较高，需要玩家投入较多的时间和金钱。因此，在选择使用刺骨时，玩家需要慎重考虑自己的实际情况和资源投入能力。对于新手玩家或者不愿意投入太多资源的玩家，建议选择其他类型的武器作为过渡或者备选方案。此外，在游戏中不断学习和提高自己的操作技巧也是非常重要的，这有助于更好地发挥武器的威力。

三、结束语

以上就是关于dnf刺骨武器的详细分析，希望能对各位玩家在选择武器时提供一些参考。无论选择何种武器，只要玩家们不断努力学习和提高自己的操作技巧，都能在游戏中取得更好的成绩。祝各位游戏愉快！

关于dnf刺骨哪个好用的介绍到此就结束了

在我们的日常生活中离不开数学，网上也有很多关于数学的游戏，那么2023数学游戏大闯关有哪些？在游戏中可以帮助玩家开发大脑的思维，还有不同的关卡，可以在这里不断的闯关，下面就是今天小编分享给大家好玩的数学游戏推荐。

1、《数独大全》

这是一款适合任何年龄段的人玩的游戏，在游戏中可以进入数字的天堂，各种不同的关卡设计，还有千变万化的数字，都能让玩家燃烧自己的大脑，在这里可以选择四宫格的数字玩法，随着越来越熟练之后，可以挑战六宫格的数字计算玩法，在每一局当中都需要在规定的时间里完成挑战，可以随着时间的紧迫性，不断的超越自己的极限，在游戏中快速的转动大脑思维。

》》》》》#数独大全#《《《《《

2、《数字运算棋》

这款游戏中可以很好的锻炼玩家的计算能力，在游戏中可以挑战不同难度的关卡，而且每一个关卡当中的玩法都不同，玩家可以操作数字在这里变魔法，运用自己独到的计算能力，可以迅速解答出需要的答案，在这里可以获得极大的成就感，加减乘除任由玩家轻松的玩转，在游戏中可以锻炼自己成为数学小天才。

》》》》》#数字运算棋#《《《《《

3、《宝宝玩数字》

这是一款及其适合小孩子的数学思维游戏，可爱的动画场景可以吸引小朋友的注意力，而且还有教读数字的玩法，在这里可以从最基础的学起，还有可爱的小动物陪伴玩家，通过小朋友去数小母鸡下的蛋等，有趣的游戏互动玩法，可以激发小朋友的兴趣，还有游泳池等不同的主题场景，可以自由的进行切换，在快乐中可以学到很多的知识，在数学小农场当中开启快乐的夏天。

》》》》》#宝宝玩数字#《《《《《

4、《奥特曼学数学》

在这款游戏中给玩家打造了一个生动有趣的学习场景，在这里有小朋友们崇拜的英雄奥特曼，可以随时进行打怪兽，但是每一个关卡当中都要计算出一定得数学题，才可以击败小怪兽，而且还有多个不同难度的等级，在这里可以激发小朋友的胜负欲，快速的掌握计算的方法，营造一个快乐的学习环境。

》》》》》#奥特曼学数学#《《《《《

5、《超级数字》

在这里玩家可以进行轻松的闯关，在游戏中结合了消除和数字的玩法，让玩家能够在游戏中掌握数学知识，还能体会到数学的魅力，每一个关卡当中都有不同难度的数学题，只需要准确的解答成功，就会成功的进行消除，就可以在这里获得一个生命值，每一次答错就会扣除一个生命值，当玩家没有生命值的时候，则会闯关失败。

》》》》》#超级数字#《《《《《

上面这几款游戏就是今天小编分享给大家的2023数学游戏大闯关推荐，在这里玩家可以体验有趣的数学世界，而且还有很多精彩的小游戏，都能轻松的尝试，让玩家可以在数字王国里度过快乐的夏天。

数学对于大部分人来说既枯燥又难学，但同时人们又能够在数学游戏中感受到数学的乐趣，于是很多人想要了解2022数学游戏有哪些。事实上，数学游戏不仅能够锻炼人们的逻辑思维能力，也能够提升人们的数学兴趣，今天小编就给大家介绍一些好玩的数学游戏，大家可以根据自己的喜好选择一款。

1、《数字领主》

《数字领主》这个游戏的玩法非常简单，在一张地图上，玩家需要从一个点开始逐渐扩张自己的领土，实现等级的提升。在这其中，并不只有简单的领土扩张，玩家还需要和其他玩家进行对抗，打败对手，感兴趣的玩家快来试试吧！

》》》》》#数字领主#《《《《《

2、《不懂数学》

《不懂数学》这个游戏额规则很简单，玩家需要将数字和运算符号运用起来，最终得到“24”这个数字。看起来好像简单，但事实并非如此，玩家们还是需要发动脑筋好好思考。

》》》》》#不懂数学#《《《《《

3、《极智脑力》

在《极智脑力》游戏中，玩家既能够提升自己的脑力，也可以增强自己的记忆能力，而且游戏还有简单、限时、困难等几种模式，受众广泛，是一款老少皆宜的益智类游戏。

》》》》》#极智脑力#《《《《《

4、《数学迷阵》

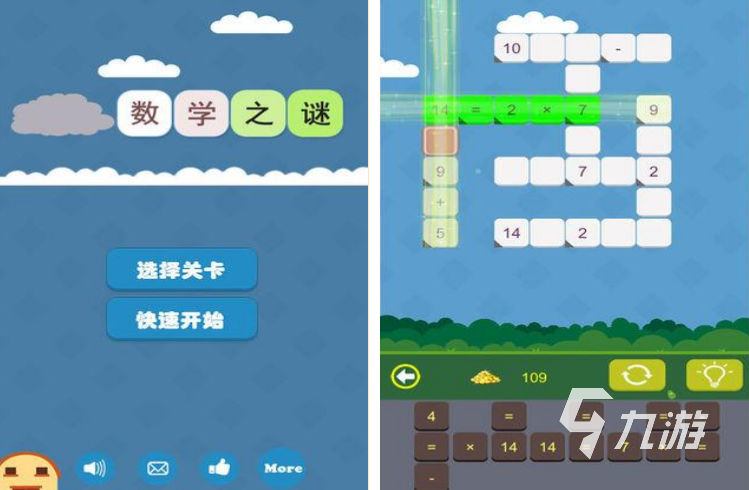
在《数学迷阵》中，玩家需要根据不同的算式来选择对应的方块，规则很简单，但玩起来并没有那么容易，还是不能轻易掉以轻心。这个游戏能够提升玩家的数学能力，以及逻辑思维能力，且游戏中涉及的小学和初中知识，特别适合学生们来巩固数学知识。

》》》》》#数学迷阵#《《《《《

5、《开心数独》

《开心数独》最主要的玩法和《数独》是一样的，只不过其中并非只有九宫格，还有更多类型的宫格，而且级别也很多，从入门到复杂，可以说是老少皆宜。

》》》》》#开心数独#《《《《《

6、《数字华容道数字方块合并》

《数字华容道数字方块合并》这个游戏包含多种益智类的游戏，比如“2048”“扫雷”“数字华容道”等等，玩家们在一个游戏里可以享受到多种游戏玩法，可以说是一种全新的体验。

》》》》》#数字华容道数字方块合并#《《《《《

7、《数学零点HD》

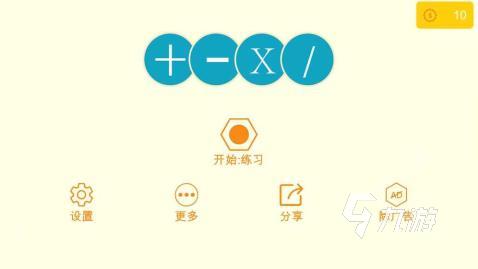
《数学零点HD》这个游戏的规则很简单，就是将数字方块和运算符运用起来，使之等于0，从而使方块全部消失。刚开始的时候数字和运算符都很少，所以很简单，但是玩到后面就会发现越来越难，所以这是一款需要玩家集中注意力，动用脑力的游戏。

》》》》》#数学零点HD #《《《《《

以上就是小编给大家推荐的2022数学游戏有哪些，这一类游戏的画面简单，需要玩家有一定的逻辑能力和思维能力，对数学游戏感兴趣的玩家还在等什么呢？赶紧点击下载来试试看吧！

雨中冒险2刺骨的拥抱是什么？想必很多朋友都不是很清楚吧，所以下面就是小编给大家带来的雨中冒险2刺骨的拥抱效果说明，需要的朋友还不快进来看看。

刺骨的拥抱效果说明

这个装备并不会出现在图鉴里面，可能是最近更新之后加上的隐藏道具？

简单的介绍一下这个道具的作用，就是让你的攻击附带特殊效果，这种道具总共有几种吧，有火属性的和电属性的。

如果不好理解的话，你可以参照游戏里面带属性的精英怪。

火属性的那个道具相当于让你拥有火属性怪的能力，而且这个道具属于被动装备，虽然放在Q键位里面，但是不能主动使用。

以上就是小编给大家带来的雨中冒险2刺骨的拥抱效果说明，想必大家都了解了吧。

在游玩《巫师3》的dlc血与酒的时候，玩家会发现一个全新的系统，能够强化自身狩魔猎人的能力。“刺骨”这个技能就是其中非常强力的一种。那么这个技能到底有什么效果，又应该怎么搭配呐？来看看“空城染指寂寞”的巫师3刺骨技能详解吧。

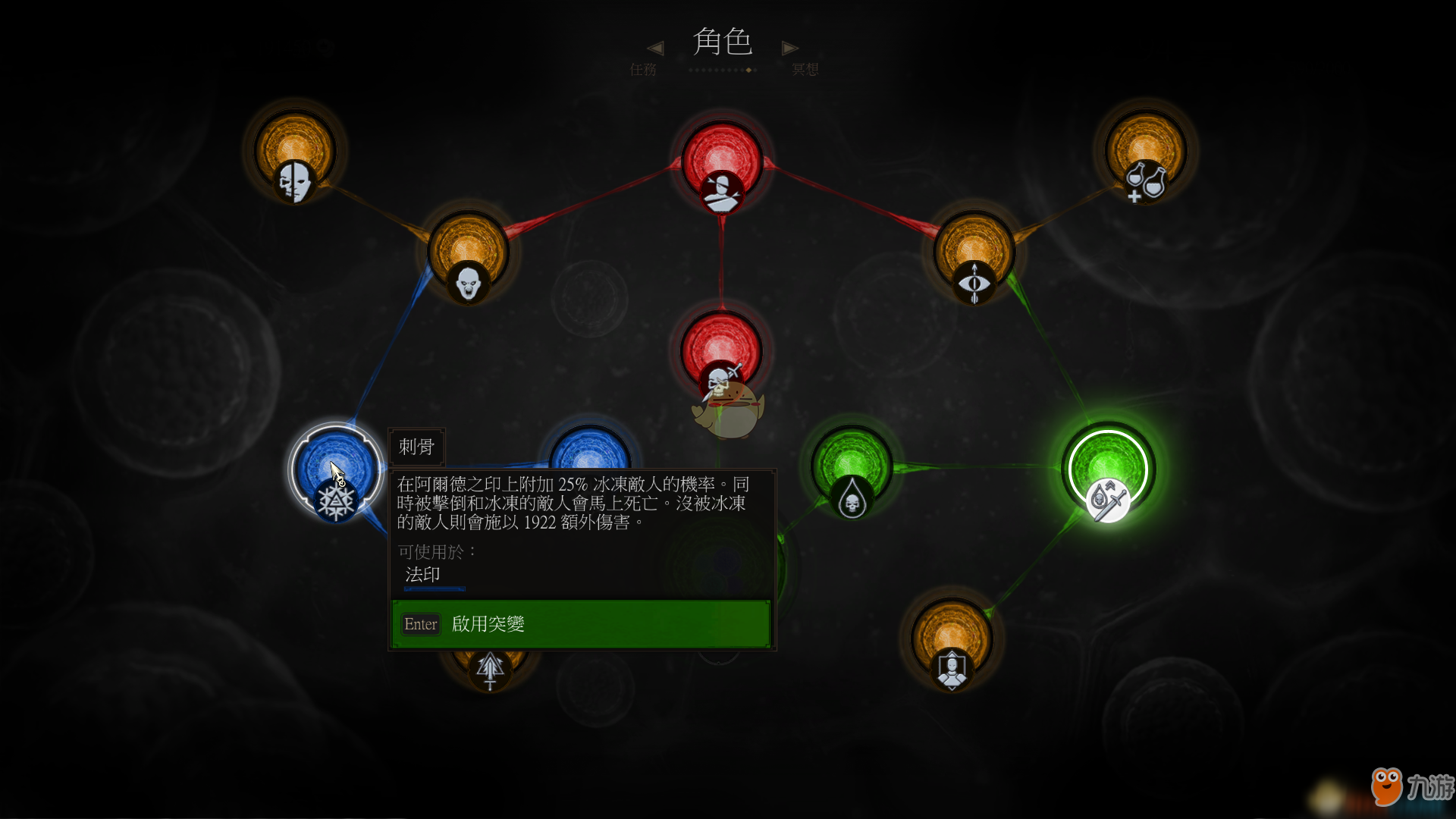
刺骨，从介绍我们可以看出来刺骨有一个立即死亡的特性而且配合法印输出可以造成高额伤害，那就意味着我们要走一条以阿尔德法印为主要输出手段配合剑术辅助的战斗路线。所以，在三种学派技巧中，我们选择了狮鹫学派，这也就意味着我们要选择中甲装备。

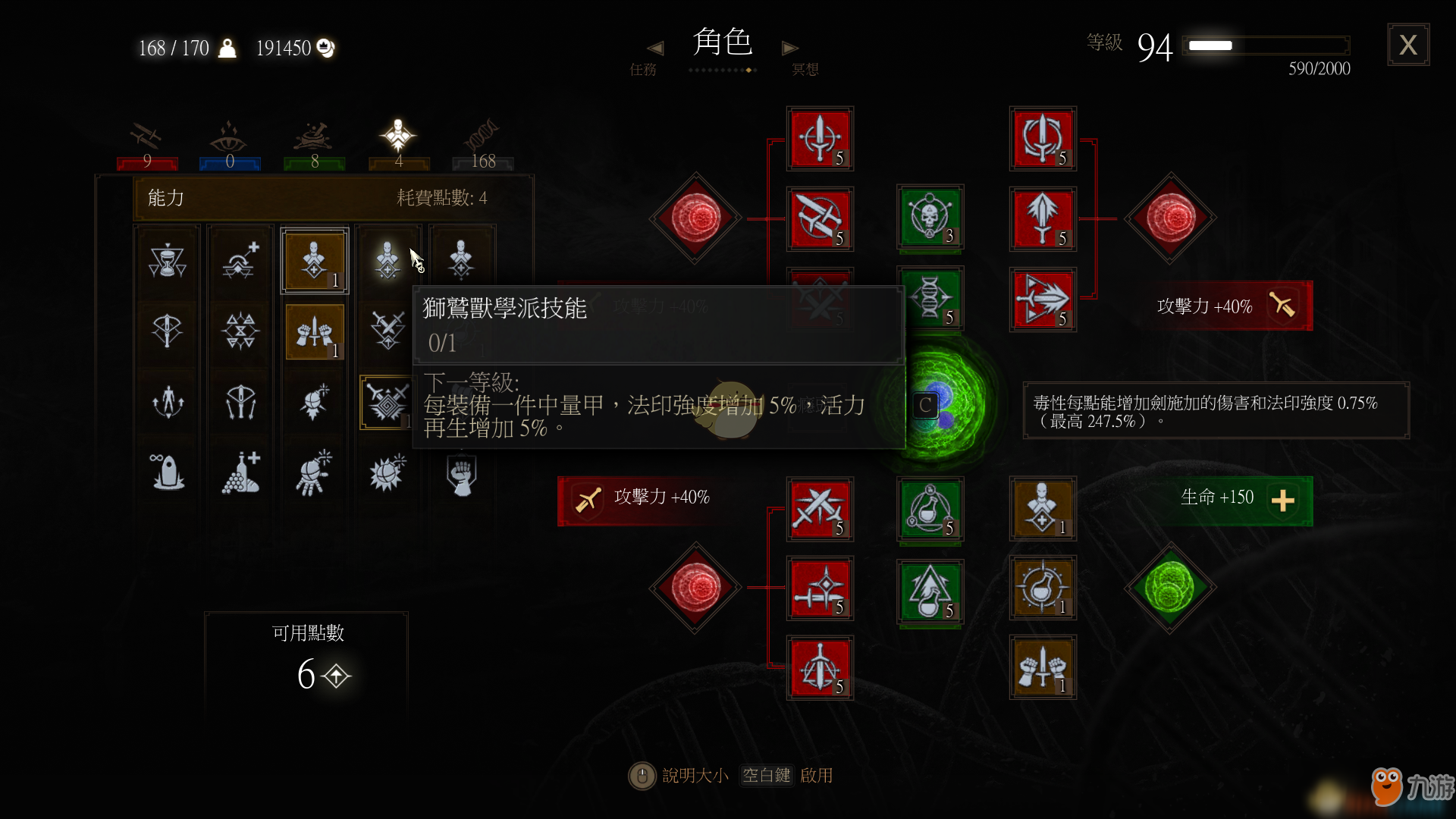
在三种毕业中量甲中狼是剑法双修，狮鹫是纯法印而飞狮并没有在法印上有所提升，所以套装选择中我们锁定了狼和狮鹫，而之所以选择了狼是因为狼套提升的剑术输出可以弥补在恢复活力的空窗期造成的伤害不足。

在技能和符文上也毫无疑问的选择增强阿尔德法印的技能和符文同时可以点出权力熏心保证阿尔德加成，以上就是刺骨狼的选择理由和思路。

今天为大家带来一个集颜值、控制、爆发为一体的中单英雄——雪女，希望能够帮助大家来学习这个新手英雄的具体玩法。

一、让我们先来研究一下雪女的技能有哪些奥秘?

被动技能：穆寒雪，该技能比较明显就是雪女用技能攻击有减速效果的敌人是会有额外的法术伤害。这使雪女在对战时尽量利用三技能减速敌人在选择释放其他攻击仅能，也可以配合一些带有减速技能的队友来增加自身的伤害。

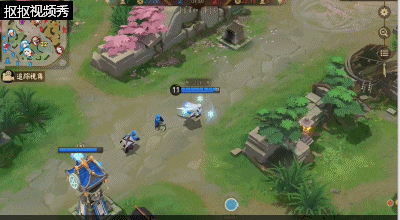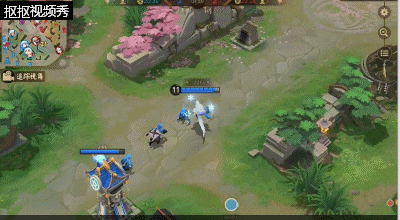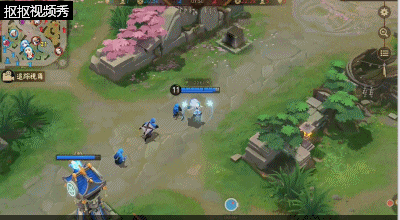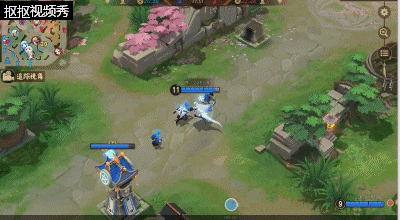
一技能：雪之妆，雪女的第二个被动技能，雪女释放技能会为自己带来一片雪花，累计获得三个自身就会生成一个护盾，护盾会在雪女受到伤害过大时破裂，并对周围的敌人带来一定的法术伤害及一段时间的定身效果。该被动在雪女被敌方式神近身攻击时，能够帮助雪女有效的逃离或发反杀。

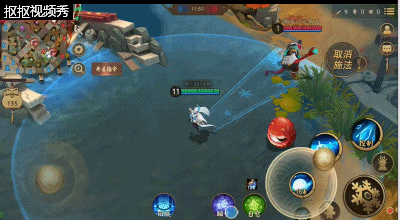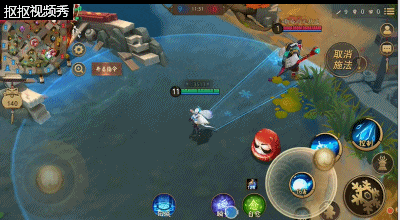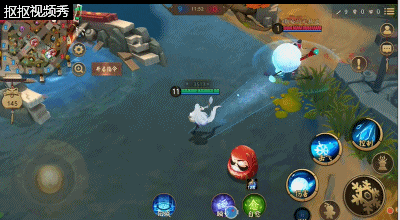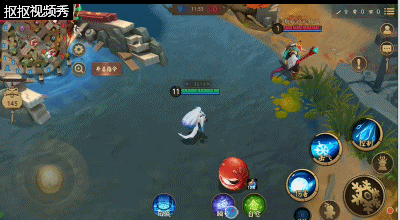
二技能：雪团子，雪女释放一团雪球，雪球会越滚越大，滚到一段距离后自动炸裂；这时对周围的敌人造成伤害，距离越远造成的伤害，但注意的是技能在触碰到敌人式神时会立刻炸裂；该技能让雪女在对线时候能够更好的抗压。

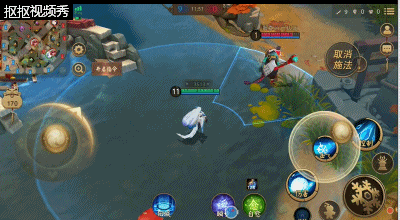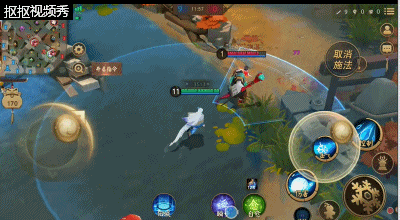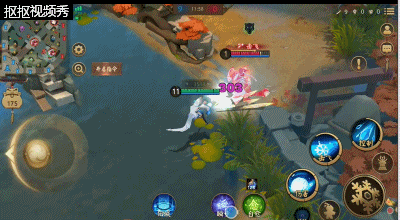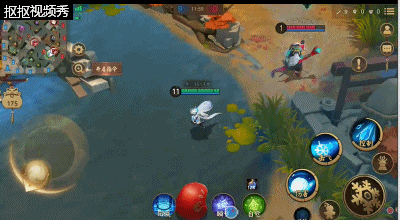
三技能：吹雪之息，该技能能够让雪女对近身的敌方式神进行击退并且会给其带俩减速效果；帮助雪女在没有位移技能是能够脱离敌方式神的追击。

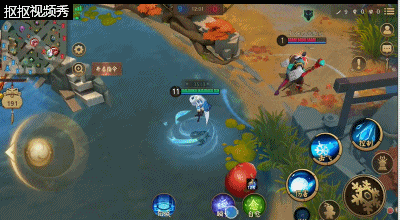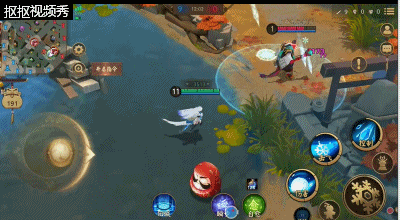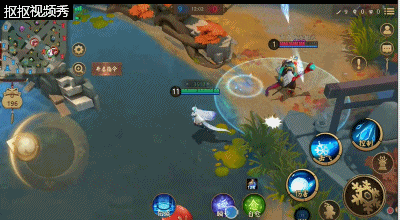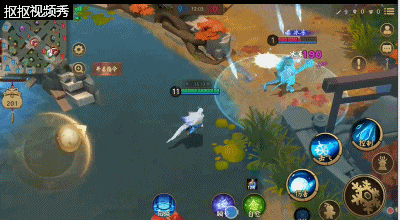
大招：霜风寒夜，该技能让雪女在打团的时候无敌的存在，强大的aoe伤害加上强大的控制能力，能够在团战中终结敌人或者逼敌方式神的走位。该技能比较可怕的就是；不管技能范围的敌方式神有多少都会被冰冻。

二、如何在对战中奖雪女的技能更好的串联起来呢？

1、单杀敌人连招：

先手一技能在敌方英雄处于该技能最大是释放将技能伤害最大化，然后接三技能减速；减速后将大招放在敌方后退的位置，对其控制并带来伤害，这时候可以在是用一技能打出输出。

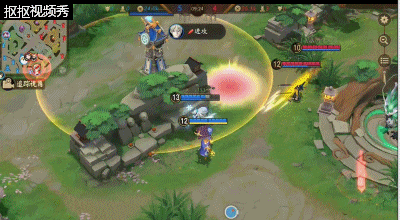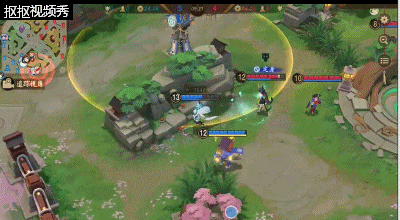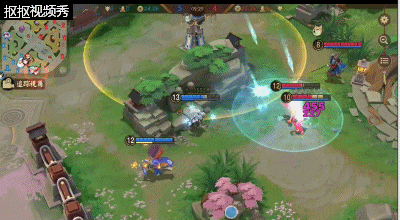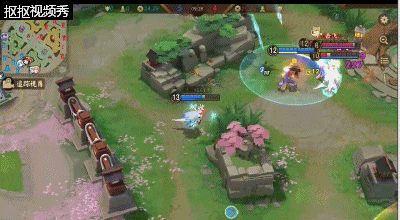
2、人近身反杀连招：

敌人近身是若是有被动则是可以通过被动护盾破裂带来的定身与敌人拉开一段距离接三技能击退并且带来减速再接大招，最后使用二技能补足伤害。如实没有被动则是尽量拉开身位，再释放三技能击退，这样能够更好的击退敌人，防止技能释放方向错误导致被击杀。

三、最适合雪女的出装是哪些？

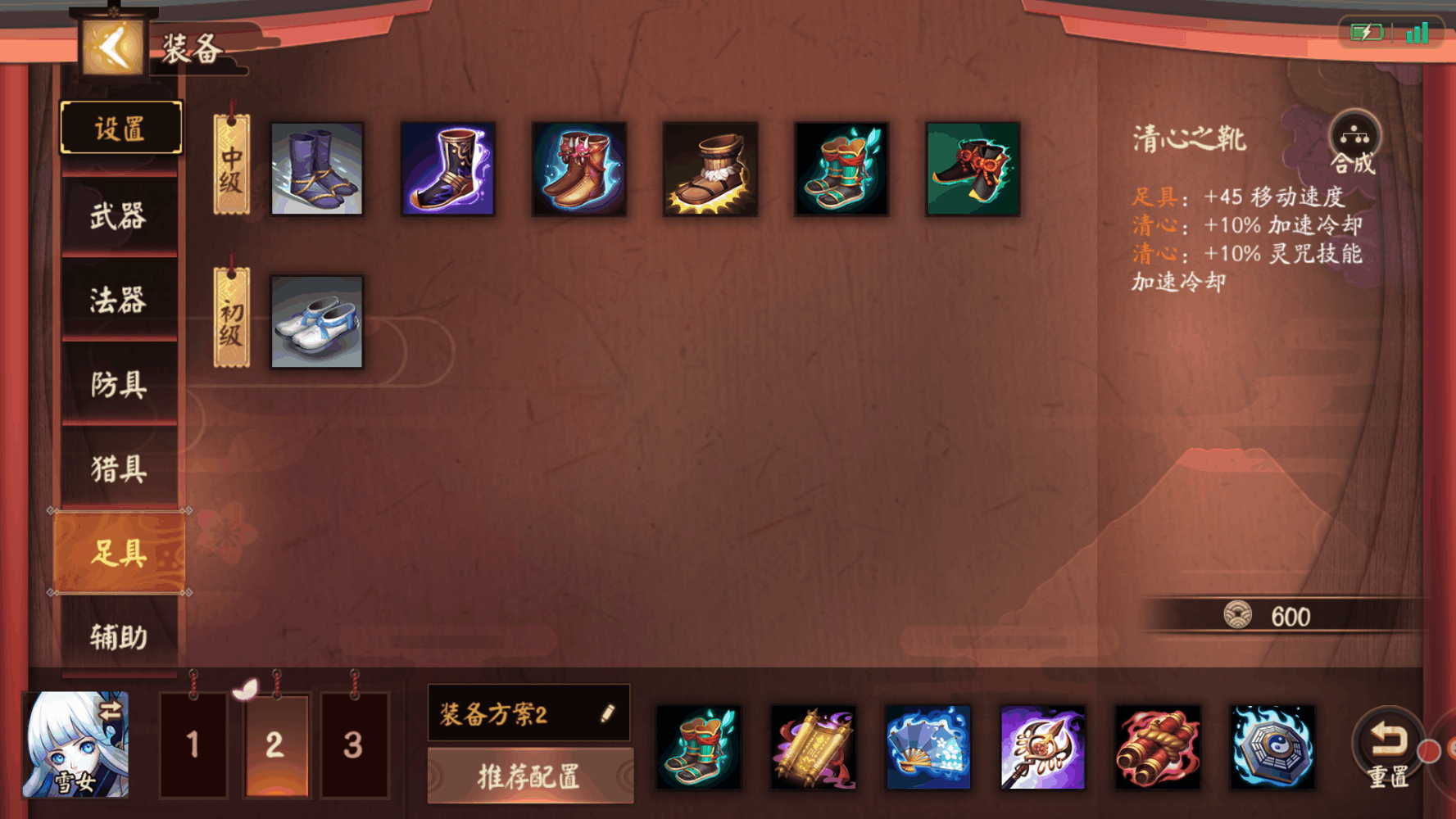
神装推荐：清心之靴、曼茶罗密经、山吹花烬、伊邪那神意、出云之章、太阴.太极

出装解析：清心之靴带来的技能冷却缩减能够帮助雪女在战斗释放更多得劲能来消耗敌人。

曼茶罗密经位雪女带来蓝量恢复和冷却时间，是雪女前期的主要装备。山吹花烬以及伊邪那神意则是增加了雪女的技能额外伤害。出云之章以及太阴.太极则是在后期增加雪女的法强以及法术穿透，打出更多的输出。后期，若是敌方刺客针对自己的话，可以古琴.须臾(yu）来增加雪女的生存力。

四、如何携带好阴阳术和灵咒？

灵咒推荐：瞬步、自愈或俊足

阴阳术选择（见下图）：

五、前期，雪女如何对线才能更好的进行发育？

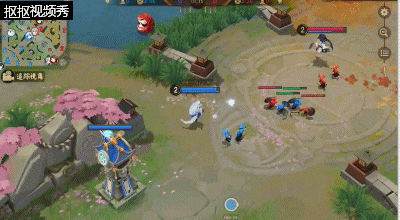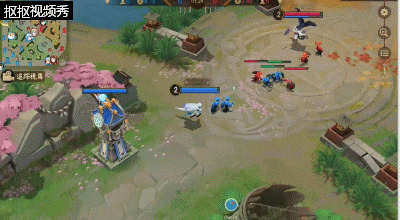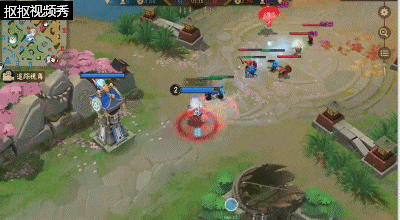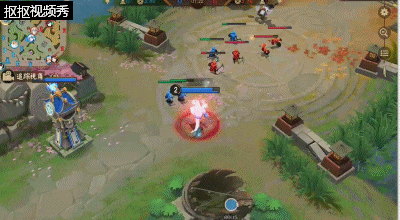
法师在前期都是比较弱势的群体，雪女也不例外；但是，雪女虽然前期输出不是很高，但是依靠二技能的远程范围攻击技能，能够快速的收割兵线并且依靠二技能的远程攻击的元婴能够在补兵的时候对敌方的中单式神进行消耗。到达三级的时候，可以先选择将雪女的一技能点出来，这样能够在一技能被动护盾激发的时候，利用技能消耗敌方式神一波，利用护盾尽量的压低敌方中单式神的血量，这样有主意自身的发育和进行游走。

六、如何在抓人GANK时，让敌人有去无回？

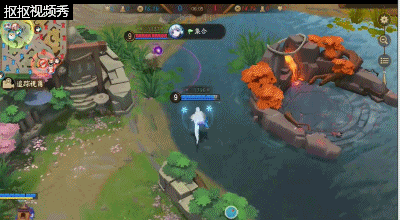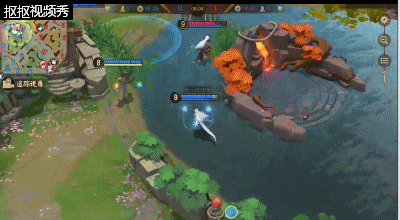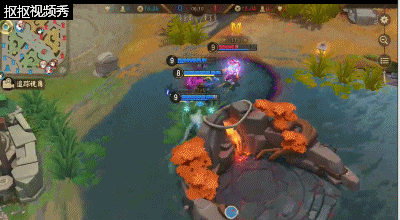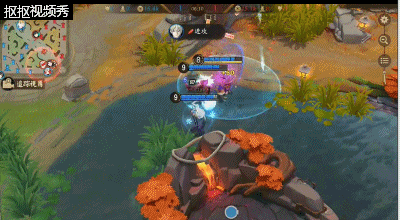
雪女在线上优势的情况下可以对其他路线的队友进行支援，在选择支援的时候一定需要注意该条路线的敌人是否过于激进或者过于深入我方，这样才能让一波GANK能够更好的触发，不然就会在支援的路线上浪费发育的时间。

在GANK是雪女可以选择直接绕后利用三技能击退想回到自家防御塔的敌方式神，在释放大招直接控制住被减速的敌方式神给到控制，在配合该路线的队友将其击杀，完成一波完美的GANK。

七、团战中，雪女该如何进行输出？

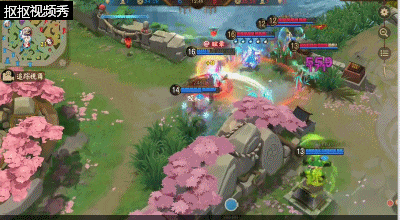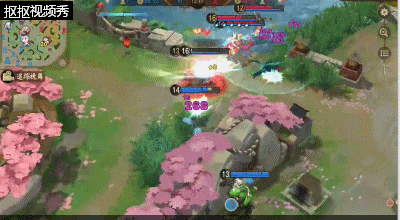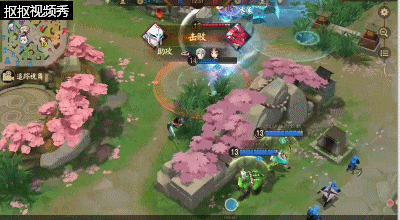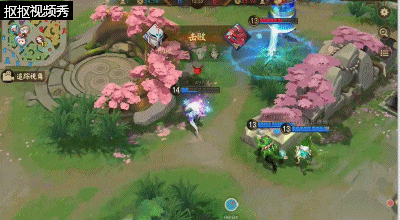
雪女作为中单输出英雄，所以在人团战中一定要注意自身的站位，处于团队中后方进行输出。

在开团前，先利用二技能进行远程消耗敌方的式神并且触发一技能的护盾效果；团战中不要轻易的打出输出而将三技能过早的用掉，这样雪女很容易被敌方的刺客类式神近身秒掉。若是，我方团战胜利面比较大或者敌方刺客类式神被我方的前排限制住时可以用三技能减速敌人来进行攻击。大招在团战中尽量放在人堆里面，这样能够控制住更多的式神获得团战的胜利，但若是敌方式神不是很集中的情况下，则是将大招尽量放在敌方的输出式神的位置进行控制或者逼走位。

「我爱数学：MathMathMath」是一款寓教于乐的数学类游戏，画风比较学院，非常适合小朋友玩，在玩游戏的过程中不知不觉学习数学知识，我爱数学，数学使我快乐~

九游括三种模式：

多人游戏：在同一个iPad或者手机上尽快点击正确的答案并收集积分，第一个拿到10分的赢得比赛。

青蛙游戏（单人游戏）：点击正确的答案则青蛙就能吃到食物，否则就会失败。

相机游戏（单人游戏）：- 同时改善你的健身和你的精神数学技能！游戏可以直接从相机图像中检测出你的动作！在相机前移动，并在空中触摸正确的答案。使用iPad智能外盖将iPad放在直立位置，然后在相机前方跳动，或将设备平放在桌子上，并将其中一根手指移动到相机前方。注意：仅适用于具有正面（面对面）相机的设备（iPad第2代和更新版，iPod第4代及更高版本）。

难得一见的寓教于乐的数学游戏，赶紧下载起来吧~

在游戏界，注重游戏技能光效已是传统，因为这样会带来华丽的感官体验。《风暴全明星》似乎并不这么想，游戏采用重物理特效的潮流动作技能，让招式融入实感的物理效果。这带来的直接后果就是在PVP和PVE的时候有了一种酣畅淋漓的感觉，透过手机屏幕，感受着自己技能带来的轻微抖动和场景的破坏，就好像能感受到刀剑相交、拳拳到肉一样，那打击感“倍儿爽”。当然，虽然是注重物理特效，但是光效同样没让人失望，各种技能效果看上去也是酷炫和华丽。

这就是《风暴全明星》，这酸爽，让人难以想象！！！

​