数学的乐趣游戏介绍
数学的乐趣简介
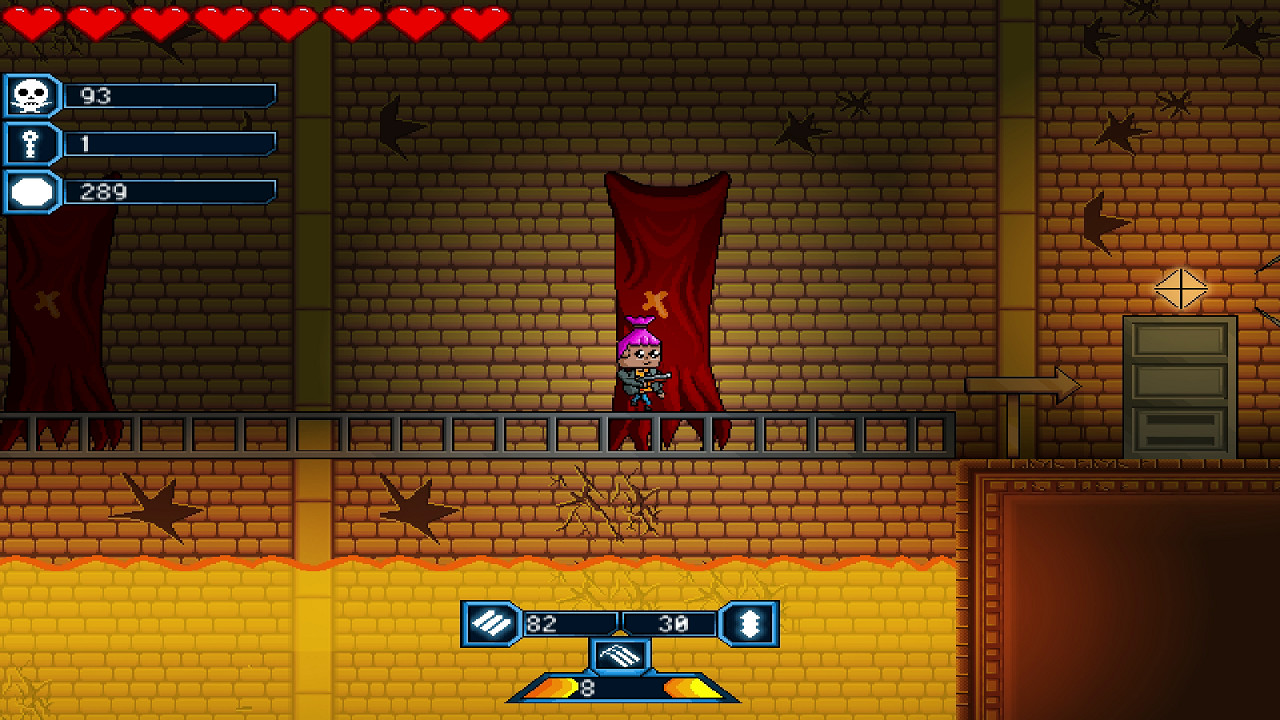
数学的乐趣游戏截图





大家都在看-热门推荐
2025年最受欢迎的数学游戏推荐:提升思维乐趣的十大必玩清单
有哪些有趣的数学游戏推荐?这些游戏将抽象的数学知识巧妙地融入到互动玩法中,让学习变得生动又轻松。通过动手操作和不断尝试,玩家可以在失败后反思调整策略,逐步掌握核心概念。不仅适合用来放松娱乐,还能在潜移默化中提升数学思维能力。无论你是想巩固基础,还是挑战逻辑极限,下面这几款游戏都值得一试。
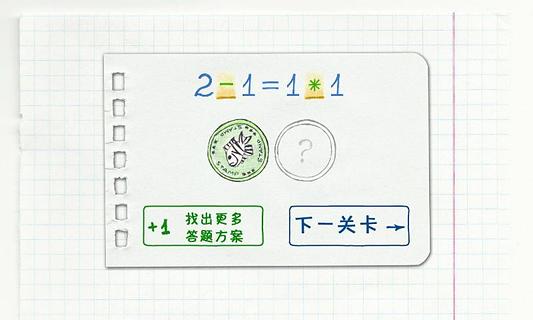
1、《数学王者赛》

该游戏融合了多个学科的知识模块,并特别强化了数学内容的设计。没有固定的操作限制,玩家需要依靠自身的分析能力和数学基础来破解各种题目。内置问答机制可根据个人表现动态调节难度,确保每位用户都能找到匹配自身水平的挑战任务。无论是练习运算技巧,还是锻炼解题思路,这款游戏都能帮助你在闯关过程中稳步提升数学素养。
》》》》》#数学王者赛#《《《《《
2、《数独清》

本作以经典数独为核心玩法,要求玩家在每行、每列以及每个小九宫格内填入不重复的数字,通过逻辑推理完成全部空格。游戏提供大量关卡,难度循序渐进,新手也能快速入门。遇到困难时可使用提示功能辅助思考,同时支持自由选择难度等级。随时随地打开即可进行一场头脑训练,是培养专注力与逻辑判断的理想选择。
》》》》》#数独清#《《《《《
3、《数学长征》
在游戏中,你将在未知星域中开启一段独特的数学旅程,面对由知识点划分的不同密室谜题。题目从基础开始逐步升级,涵盖计算、逻辑推理与策略规划等多个维度,前后关卡紧密关联。无时间压力,也无需额外付费,利用碎片时间即可沉浸于解谜过程。一边探索宇宙奥秘,一边提升思维敏捷度,体验寓教于乐的乐趣。
》》》》》#数学长征#《《《《《
4、《奇妙数字农场》

这是一款结合农业经营与数学训练的游戏。种植作物前必须正确解答对应的加减法问题,播种阶段每种植物对应特定数学挑战,只有解出才能继续。日常农活也需要答题获取升级资源,用于解锁新设施和作物类型。此外还有限时竞赛模式,在规定时间内解答越多题目,收获越丰富,并可与其他玩家比拼成绩。在轻松氛围中实现边玩边学,悄然增强数学应用能力。
》》》》》#奇妙数字农场#《《《《《
5、《数独大全》

该游戏集成了数字记忆与逻辑推理解谜元素,界面简洁直观,配有舒缓的背景音乐。难度划分为多个层级,每一级都有独特挑战目标。玩家需在限定区域内填写数字,既要填满所有空白格,又要保证每行每列及每个区块内的数字不重复。长期游玩有助于提升对数字的敏感性,强化逻辑推理能力,是锻炼大脑灵活性的好方式。
》》》》》#数独大全#《《《《《
6、《数学女神》
玩家可自定义角色并进入一个充满数学挑战的奇幻世界。在冒险途中会遭遇各类算术难题,成功解答后可获得经验值与实用道具,用于增强角色属性。随着属性积累,还能解锁更多高级运算技能。对于觉得传统学习枯燥的人来说,这款游戏提供了全新的互动体验,在享受剧情推进的同时,持续锻炼数学解题能力,适合希望换种方式学习的人群尝试。
》》》》》#数学女神#《《《《《
7、《脑洞消数字》

这款作品将数学元素与消除类玩法相结合,规则简单易懂,无需复杂学习即可上手。包含多种经典模式和大量关卡,随着进度推进,挑战逐渐加大。它把原本单调的数学运算转化为清晰的消除目标,在游戏中提升反应速度与心算能力。无论是想边娱乐边接触数学知识,还是单纯享受消除带来的快感,这里都能满足你的需求。
》》》》》#脑洞消数字#《《《《《
以上就是关于数学游戏有哪些的相关介绍。这些游戏不仅能激发对数字的兴趣,还能在持续挑战中锻炼逻辑思维与运算能力。通过层层递进的任务设计,让人在不知不觉中掌握规律、建立信心。即使原本对数学缺乏热情,也能在游戏中收获成就感,发现学习的新路径,轻松迈入数学世界的奇妙大门。
经典的5~6年级的趣味数学游戏大全 2025有趣的数学游戏排行
5~6年级的趣味数学游戏有什么?当充满乐趣的游戏遇见好玩的数学世界,会产生出怎样令人惊喜的娱乐火花呢?这些游戏都是以不同的数学原理为基础,精心打造出趣味满满的玩法。真心希望小朋友们都能去试一试,在游戏中尽情享受快乐时光。相信每一位小朋友在参与这些有趣的数学游戏时,都能收获满满的欢乐。
1、《数字拼图》

游戏将传统数字益智玩法与巧妙谜题设计结合一起。游戏中由一个个小方格构成挑战的地方,玩家需依据左侧和上方的数字提示,在对应方格内放置圆形标记。当所有数字都准确归位,一幅精美的画面便会如魔法般渐渐浮现。游戏关卡设计丰富多样,难度呈阶梯式递增,从非常简单的入门关卡,到检验智力的高难度挑战,满足不同玩家的想法。每次成功解开谜题,都是对玩家智慧的一次嘉奖,同时也为迎接更高难度的挑战筑牢根基。
》》》》》#数字拼图#《《《《《
2、《数独谜题挑战》
游戏为玩家精心准备了众多趣味的数字解谜关卡,包含多个数独谜题挑战,每一关的难度都各不相同。从最基础的关卡入手,逐步积累游戏经验,这样在后续的挑战中才能更加轻松手,最终顺利地通关。游戏设计了许多不同的题目类型,形成了不同层次的难度体系。玩家可以按照自己的节奏,逐步征服每一个关卡,享受挑战自我的乐趣。没有额外的道具助力,完全依靠玩家的智慧和操作技巧来解开谜题,感受数学的独特魅力。
》》》》》#数独谜题挑战#《《《《《
3、《几何谜题》

以数学几何为灵感的益智类手机游戏,巧妙运用简单的数学坐标点与线段,构建出各式各样的图形谜题,激发玩家对图形的洞察力与解题思维的灵活性。游戏中设计了多样化的几何挑战关卡,让玩家在探索许多数学谜题的过程中,领略到线段和立体图形的千变万化。此外,游戏还内置了社交功能,玩家可以与朋友们一起探讨数学解题策略,分享几何知识的心得。整体操作直观易懂,更侧重于培养孩子们的几何思维与实际能力。
》》》》》#几何谜题#《《《《《
4、《儿童益智数学》

玩家们能在愉快的氛围中迎接各种趣味挑战,通过游戏获得真实的算术实践体验。游戏巧妙融合了生动的动画元素与数字知识,助力孩子们在玩乐中拓展思维边界。情景互动模式的设计,让孩子们仿佛置身于数学的世界,以趣味的方式探索数学的奥秘,每过一关都是对数学认知的一次深化。精心打造的各个关卡,不仅富有挑战性,还充满了乐趣。游戏还提供了沉浸式的学习场景,搭配着设计巧妙的图片,以及寓教于乐的故事情节,让数学学习变得生动有趣。
》》》》》#儿童益智数学#《《《《《
5、《我的数学大赛》
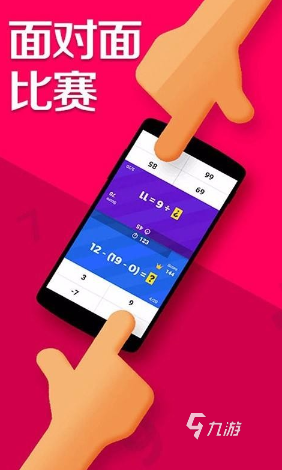
玩家可以通过解答算术题目来迅速得出答案并作出选择,游戏的主界面设计得十分简洁,只需轻轻一点开始,系统便会自动为玩家匹配适合的题目,让玩家马上投身于刺激的竞赛之中。此外,游戏还包含了在线与离线两种比赛模式供玩家选择,满足不同场景下的游戏需求。还贴心地准备了个性化的彩色背景,使得游戏主题更加鲜明,前景内容也更为突出。无需掌握任何复杂的操作技巧,只要数学运算能力足够出色,就能在游戏中非常轻松,享受运算带来的乐趣。
》》》》》#我的数学大赛#《《《《《
6、《算数我最会》

游戏运用寓教于乐的方式,帮助玩家们在轻松愉快的氛围中掌握数学知识,同时锻炼玩家的逻辑思维与脑力发展。游戏不仅能让孩子们在玩耍中享受乐趣,还能自动记录他们的游戏表现与进步轨迹,以此激发孩子们持续学习的动力。还具备成绩分享与排行榜功能,玩家们可以邀请好友一起参与,通过比拼成绩来增加互动与趣味性。此外,游戏内提供了多样的主题背景和音效选择,让游戏体验更加多彩。采用了经典的挑战模式,关卡难度会逐步提升,为玩家们带来持续的新鲜感与挑战性。
》》》》》#算数我最会#《《《《《
7、《数学长征》
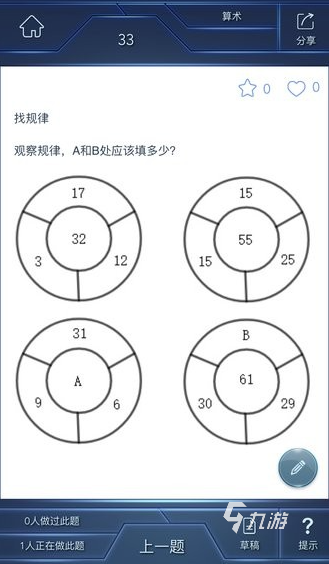
创新地将数学知识巧妙融入游戏环节,玩家能够以闯关探险的形式开启数学学习之旅。游戏内的题目类型多样,所涉及的知识范畴极为广泛,从基础概念到复杂应用均有涵盖。每道题目都配备有细致入微的知识点讲解,让玩家在享受游戏乐趣的过程中,不知不觉地提升数学能力。玩家将化身为勇敢的探索者,踏上一段充满挑战与惊喜的数学冒险征程。当玩家在游戏中不断摸索,逐渐掌握高效学习数学的方法,能够顺利攻克一个又一个难关。
》》》》》#数学长征#《《《《《
孩子们在玩这些5~6年级的趣味数学游戏的过程中,能够在轻松愉悦的氛围里,不知不觉地促进智力的发育和提升。它们不仅趣味十足,还设置了丰富多样的关卡,让小朋友们在挑战中感受游戏的魅力,收获愉悦的体验。
我数学特强《我数学特强》通解是存在的
我数学特强《我数学特强》通解是存在的!如下:
《我数学特强》有没有万能公式呢?很久之前,一开始玩的时候,就想过这个问题,但面对复杂的变换路径,我完全没有头绪。
最近的研究让我找到了通用的解法,这不是用程序暴力搜索答案,也不是简要的技巧,而是公式化的解法。另外,游戏里要求使用最少步数的最优解,而通解一般不限步数。
介绍一下游戏。有三个自然数,玩家每次操作可以对这三个数进行分配,我称为偶变换和奇变换,偶变换是把一个偶数减半并将减半的部分加到另一个数上,奇变换是把一个奇数加到另一个数上,然后将其变为0。实际上,奇变换不限奇数,因为将偶数奇变换给另一个数,可以先一直偶变换直到变为奇数,再进行奇变换。游戏的最终目标是得到三个相等的数,用三元数组表示为{x, x, x},不过显然只要三个数里有x或2x就能得到{x, x, x}。
有通解的前提是有解,而有解的充要条件是,三个数的最大公约数g整除x(可表示为g|x),且三个数不是一零二奇。先证明必要性,og和og'分别为三个数变换前后的最大奇公约数,易证og|og',如果og'=x,则og|x,也就是说如果得到了{x,x,x},则有og|x,因此og|x是有解的必要条件。另外,由g=(a,b,c)(三个数a,b,c的最大公约数写法为(a,b,c)),可得g|3x,令g=og*2^m,则(og*2^m)|3x,(2^m)|(3x/og),而(2^m,3)=1,所以(2^m)|(x/og),(og*2^m)|x,可得g|x也是有解的必要条件,其逆否命题为,若g不整除x,则无解,而(0,0,3x)不整除x,一零两奇时只能奇变换为{0,0,3x},两者等价,所以三数不是一零两奇也是有解的必要条件。至于充分性,如果我们找到了g|x且不是一零两奇情况下的解法,就相当于将其证明了。
通解讨论的数组默认已通过以上判别法筛选,以保证有解及证明充分性。但要注意,有解的数组在变换后不一定有解,通解的操作应当保证数组在变换后依然可解,时刻有g|x。
下面的是我早期想的通解,经过计算机验证,x为奇数时,x>17后出现反例:
一、有x或2x则结束。
三、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择三种操作进行后g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分配给两奇数使其变为两偶数,选择两种操作进行后g整除x的数组。
四、若数组中没有g*2^k满足g*2^k>=x,k是自然数,则不断在两正数之间进行偶变换(如果x是偶数,则需要保证两数都是偶数),如果找到g*2^k,则跳到步骤六。
五、在步骤四的循环中选择含有数被4整除得奇数(且该数减半小于x)的数组(如果x是偶数则选择被2整除的),将该数偶变换给0,再重新在两数之间不断进行偶变换(如果x是偶数,则需要保证两数都是偶数),出现g*2^k则结束,将另两个数合并。
六、用二进制数表示x/g,在左边补充0直到位数等于k,从最高位到最低位,若为1则将g*2^k分配给0(或者是步骤五中得到g*2^k一半的数),为0则分配给另一个数。这样就得到了x,结束。
虽然有很多漏洞,但大框架是对的。在下文逐步分析后,我们将会推导出一个正确的通解。
直接得到通解可能是困难的,于是我想着要不然先解决什么样的组合是可解的问题吧。反复观察变换路径后,我猜测g整除x应该和有解相关,并且还发现了og在变换的过程中不变或变大,而且变换后的og整除变换前的og。
然后,我再想的是解决相对简单的数组。在三个数之间变换是复杂的,暂未发现规律,所以我研究了只有一个数为0的数组。如果三个正数的数组都能转变为一零两正,那么通解问题就可以归约到一零两正如何变换出x或2x的问题。
我们需要保证三正变两正后,g依然满足g|x。如何操作呢?对于{a,b,c},奇变换后得到的{0,a+b,c}, {0,b,a+c}和{a,0,b+c}三个数组中,一定有一个数组的g满足g|x。
证明:3x的质因数分解为m*3^n,(m,n)=1。先假设三个数组的g都不整除x。(a+b,c)=(3x,c),(a+c,b)=(3x,b),(b+c,a)=(3x,a)如果都不整除x,则(3^n)|(a,b,c),又因为(a,b,c)|x,可得(3^n)|x,但3x=m*3^n,(m,3)=1,矛盾。
两奇一偶时(该偶数不为0),以上的三种操作可能会让数组变为一零两奇,因此我们要对该类情况作调整,它有两种变换:一、两奇相加;二、偶数拆分为两奇数,分别加给另外两奇数。这两种变换会使三正变一零两偶,且至少有一种使得g|x,证明类似上一个,不再赘述。这样的话,我们就将前面提到的可解的数组都转化为一零两正了。
前面说过{0,0,3x}是无解的,两个正数不能奇变换,那当然就只好偶变换了。当x为奇数时,两个数一奇一偶,偶变换的对象(即哪个数给另一个数一半)是确定的,得到的下一数组是唯一的。再加上数组的和是不变的,这样的数组个数有限,所以,经过有限次偶变换后,一定会回到原来的数组,形成偶变换循环。当x为偶数时,偶变换的路径是不唯一的,且不一定能不断偶变换,变换后还可能是一零两奇,比如{2,10}。x为偶数的这种情况,后续在改进偶变换的时候再提及。
我们的目标是在循环中找到t*2^k,t*2^k>=x,t|x,k>0,因为在有三个数时,将t*2^k偶变换分解,可以得到小于t*2^k任意一个自然数。但循环中并不一定有t*2^k(比如{5,28}),所以在早期的想法中,我想打破原有循环,把偶数偶变换分给第三个数,使得原来循环的两个数进入新的循环,以找到t*2^k。
在{a,b}的偶变换循环中,如果我们只关注其中一个数a,可以发现该数在作如下变换:偶数时减半,奇数时加上sum再减半,sum=a+b。冰雹猜想里的变换会迭代至2^k,而这里,迭代至t*2^k,a和sum要满足的所有条件是什么,是个open的问题。修改了几次进入新循环的方法后,程序依然发现反例。所以,探寻如何修正a和sum进入新的含有t*2^k的循环,这条路暂时行不通。
不小于x的t*2^k一定和小于x的t*2^k在同一循环中,找到其中一个便能找到其余的t*2^k。但要得到新的循环,就要将参与偶变换循环的两数之和sum减小,而最大的t*2^k满足t*2^k
这样我们就有一个新的思路,先找到小于x的t*2k,再保持t*2^k不变,将sum增大使得sum>2x,进行新一轮偶变换,得到不小于x的t*2^k。
在偶变换时,如果偶数减半后还是偶数,则将这一部分加到第三个数上,这样我们就将前面总和不变的循环改成了总和递减的。由于无论怎么变换三个数都必为自然数,循环的总和不能无限递减,那它的下界是多少呢?当不能再分配给第三个数时,总和不变,因此偶变换一次,对象就交换,此后的所有偶数除以2后都为奇数,假设(a,b)中a为偶数,此时偶数a的变换如下:
a
a/2
a/4+sum
a/8+sum/2
a/16+sum/4+sum
a/32+sum/8+sum/2
a/64+sum/16+sum/4+sum
...
第n个偶数和第n-1偶数的递推式为x_n+1=x_n/4+sum,x_0=a
可得通式x_n=(a-4sum/3)/4^n+4sum/3
当a>4sum/3时,x_n单调递增,当a<4sum/3时,x_n单调递减,数组的大小是有限的,不能单调递增或递减,因此a=4sum/3=2a/3+2b/3,可得a=2b,偶变换循环的过程中,a和b的最大奇公约数og始终不变,又因为b是奇数,b和2b的最大奇公约数为b,所以,当sum最小时,a=2b=2og。前面的三正变两正保持了g|x,所以b|x。
当x为奇数时,将{b,2b,3x-3b}转化为{b,3x-2b,0},再对两正数偶变换即可得到t*2^k<=3x<=t*2^(k+1),此时的t*2^k>=3x/2>x,可进行二进制分配。不过,我们不必操作至sum递减至3b,如果过程中出现了t*2^k,若其不小于x自然不用说,若小于x,则将另两个数合并再偶变换就能得到不小于x的。
当x为偶数时,3x-3b为奇数,如果a>=x,则a二进制分配即可得x,如果a
t*2^k>=(3x-b)/2>=5x/4>x。同样地,我们不一定要等sum减到3b,出现小于x的t*2^k时,t*2^k一定是循环中最大的,大于与它偶变换的奇数u,设第三个数为v,v是奇数,则由t*2^k
综上,我们得到了一个通解:
一、有x或2x则结束。
二、数组中是否有q=t*2^k,其中t|x,且q>x,k>0(第一次找到q或者q>x,需要将另两数合并),是则将q以外的另两个数合并,跳至六
三、是否q
四、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择其中g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分成奇数给两奇数,选择其中g整除x的数组。
五、进行步骤一二三,若偶变换的数不是偶数,则交换对象,一个偶数减半后,若参与偶变换的两个数不都是奇数,则不断进行偶变换,否则分配给第三个数(如果已经找到q则永远不再分配给第三个数),继续五。
六、用二进制数表示x/t,在左边补充0直到位数等于k,从最高位到最低位,若为1则将q分配给0,为0则分配给另一个数。这样就得到了x,结束。
至此,我们从理论上推导证明了通解的可行性,此外,我还写了验证该解法的cpp代码,对0<=x<=1000的所有有解数组都进行了验证并且验证成功。
当然,也许还存在其他通解,我很期待看到新想法。
我数学特强《我数学特强》通解是存在的
我数学特强《我数学特强》通解是存在的!如下:
《我数学特强》有没有万能公式呢?很久之前,一开始玩的时候,就想过这个问题,但面对复杂的变换路径,我完全没有头绪。
最近的研究让我找到了通用的解法,这不是用程序暴力搜索答案,也不是简要的技巧,而是公式化的解法。另外,游戏里要求使用最少步数的最优解,而通解一般不限步数。
介绍一下游戏。有三个自然数,玩家每次操作可以对这三个数进行分配,我称为偶变换和奇变换,偶变换是把一个偶数减半并将减半的部分加到另一个数上,奇变换是把一个奇数加到另一个数上,然后将其变为0。实际上,奇变换不限奇数,因为将偶数奇变换给另一个数,可以先一直偶变换直到变为奇数,再进行奇变换。游戏的最终目标是得到三个相等的数,用三元数组表示为{x, x, x},不过显然只要三个数里有x或2x就能得到{x, x, x}。
有通解的前提是有解,而有解的充要条件是,三个数的最大公约数g整除x(可表示为g|x),且三个数不是一零二奇。先证明必要性,og和og'分别为三个数变换前后的最大奇公约数,易证og|og',如果og'=x,则og|x,也就是说如果得到了{x,x,x},则有og|x,因此og|x是有解的必要条件。另外,由g=(a,b,c)(三个数a,b,c的最大公约数写法为(a,b,c)),可得g|3x,令g=og*2^m,则(og*2^m)|3x,(2^m)|(3x/og),而(2^m,3)=1,所以(2^m)|(x/og),(og*2^m)|x,可得g|x也是有解的必要条件,其逆否命题为,若g不整除x,则无解,而(0,0,3x)不整除x,一零两奇时只能奇变换为{0,0,3x},两者等价,所以三数不是一零两奇也是有解的必要条件。至于充分性,如果我们找到了g|x且不是一零两奇情况下的解法,就相当于将其证明了。
通解讨论的数组默认已通过以上判别法筛选,以保证有解及证明充分性。但要注意,有解的数组在变换后不一定有解,通解的操作应当保证数组在变换后依然可解,时刻有g|x。
下面的是我早期想的通解,经过计算机验证,x为奇数时,x>17后出现反例:
一、有x或2x则结束。
三、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择三种操作进行后g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分配给两奇数使其变为两偶数,选择两种操作进行后g整除x的数组。
四、若数组中没有g*2^k满足g*2^k>=x,k是自然数,则不断在两正数之间进行偶变换(如果x是偶数,则需要保证两数都是偶数),如果找到g*2^k,则跳到步骤六。
五、在步骤四的循环中选择含有数被4整除得奇数(且该数减半小于x)的数组(如果x是偶数则选择被2整除的),将该数偶变换给0,再重新在两数之间不断进行偶变换(如果x是偶数,则需要保证两数都是偶数),出现g*2^k则结束,将另两个数合并。
六、用二进制数表示x/g,在左边补充0直到位数等于k,从最高位到最低位,若为1则将g*2^k分配给0(或者是步骤五中得到g*2^k一半的数),为0则分配给另一个数。这样就得到了x,结束。
虽然有很多漏洞,但大框架是对的。在下文逐步分析后,我们将会推导出一个正确的通解。
直接得到通解可能是困难的,于是我想着要不然先解决什么样的组合是可解的问题吧。反复观察变换路径后,我猜测g整除x应该和有解相关,并且还发现了og在变换的过程中不变或变大,而且变换后的og整除变换前的og。
然后,我再想的是解决相对简单的数组。在三个数之间变换是复杂的,暂未发现规律,所以我研究了只有一个数为0的数组。如果三个正数的数组都能转变为一零两正,那么通解问题就可以归约到一零两正如何变换出x或2x的问题。
我们需要保证三正变两正后,g依然满足g|x。如何操作呢?对于{a,b,c},奇变换后得到的{0,a+b,c}, {0,b,a+c}和{a,0,b+c}三个数组中,一定有一个数组的g满足g|x。
证明:3x的质因数分解为m*3^n,(m,n)=1。先假设三个数组的g都不整除x。(a+b,c)=(3x,c),(a+c,b)=(3x,b),(b+c,a)=(3x,a)如果都不整除x,则(3^n)|(a,b,c),又因为(a,b,c)|x,可得(3^n)|x,但3x=m*3^n,(m,3)=1,矛盾。
两奇一偶时(该偶数不为0),以上的三种操作可能会让数组变为一零两奇,因此我们要对该类情况作调整,它有两种变换:一、两奇相加;二、偶数拆分为两奇数,分别加给另外两奇数。这两种变换会使三正变一零两偶,且至少有一种使得g|x,证明类似上一个,不再赘述。这样的话,我们就将前面提到的可解的数组都转化为一零两正了。
前面说过{0,0,3x}是无解的,两个正数不能奇变换,那当然就只好偶变换了。当x为奇数时,两个数一奇一偶,偶变换的对象(即哪个数给另一个数一半)是确定的,得到的下一数组是唯一的。再加上数组的和是不变的,这样的数组个数有限,所以,经过有限次偶变换后,一定会回到原来的数组,形成偶变换循环。当x为偶数时,偶变换的路径是不唯一的,且不一定能不断偶变换,变换后还可能是一零两奇,比如{2,10}。x为偶数的这种情况,后续在改进偶变换的时候再提及。
我们的目标是在循环中找到t*2^k,t*2^k>=x,t|x,k>0,因为在有三个数时,将t*2^k偶变换分解,可以得到小于t*2^k任意一个自然数。但循环中并不一定有t*2^k(比如{5,28}),所以在早期的想法中,我想打破原有循环,把偶数偶变换分给第三个数,使得原来循环的两个数进入新的循环,以找到t*2^k。
在{a,b}的偶变换循环中,如果我们只关注其中一个数a,可以发现该数在作如下变换:偶数时减半,奇数时加上sum再减半,sum=a+b。冰雹猜想里的变换会迭代至2^k,而这里,迭代至t*2^k,a和sum要满足的所有条件是什么,是个open的问题。修改了几次进入新循环的方法后,程序依然发现反例。所以,探寻如何修正a和sum进入新的含有t*2^k的循环,这条路暂时行不通。
不小于x的t*2^k一定和小于x的t*2^k在同一循环中,找到其中一个便能找到其余的t*2^k。但要得到新的循环,就要将参与偶变换循环的两数之和sum减小,而最大的t*2^k满足t*2^k
这样我们就有一个新的思路,先找到小于x的t*2k,再保持t*2^k不变,将sum增大使得sum>2x,进行新一轮偶变换,得到不小于x的t*2^k。
在偶变换时,如果偶数减半后还是偶数,则将这一部分加到第三个数上,这样我们就将前面总和不变的循环改成了总和递减的。由于无论怎么变换三个数都必为自然数,循环的总和不能无限递减,那它的下界是多少呢?当不能再分配给第三个数时,总和不变,因此偶变换一次,对象就交换,此后的所有偶数除以2后都为奇数,假设(a,b)中a为偶数,此时偶数a的变换如下:
a
a/2
a/4+sum
a/8+sum/2
a/16+sum/4+sum
a/32+sum/8+sum/2
a/64+sum/16+sum/4+sum
...
第n个偶数和第n-1偶数的递推式为x_n+1=x_n/4+sum,x_0=a
可得通式x_n=(a-4sum/3)/4^n+4sum/3
当a>4sum/3时,x_n单调递增,当a<4sum/3时,x_n单调递减,数组的大小是有限的,不能单调递增或递减,因此a=4sum/3=2a/3+2b/3,可得a=2b,偶变换循环的过程中,a和b的最大奇公约数og始终不变,又因为b是奇数,b和2b的最大奇公约数为b,所以,当sum最小时,a=2b=2og。前面的三正变两正保持了g|x,所以b|x。
当x为奇数时,将{b,2b,3x-3b}转化为{b,3x-2b,0},再对两正数偶变换即可得到t*2^k<=3x<=t*2^(k+1),此时的t*2^k>=3x/2>x,可进行二进制分配。不过,我们不必操作至sum递减至3b,如果过程中出现了t*2^k,若其不小于x自然不用说,若小于x,则将另两个数合并再偶变换就能得到不小于x的。
当x为偶数时,3x-3b为奇数,如果a>=x,则a二进制分配即可得x,如果a
t*2^k>=(3x-b)/2>=5x/4>x。同样地,我们不一定要等sum减到3b,出现小于x的t*2^k时,t*2^k一定是循环中最大的,大于与它偶变换的奇数u,设第三个数为v,v是奇数,则由t*2^k
综上,我们得到了一个通解:
一、有x或2x则结束。
二、数组中是否有q=t*2^k,其中t|x,且q>x,k>0(第一次找到q或者q>x,需要将另两数合并),是则将q以外的另两个数合并,跳至六
三、是否q
四、若三数都是正数,且不是两奇一偶,则尝试将其中一个数加给另外两个数中的一个数,选择其中g整除x的数组;若三数都是正数,且两奇一偶,则将两奇数相加,或将偶数分成奇数给两奇数,选择其中g整除x的数组。
五、进行步骤一二三,若偶变换的数不是偶数,则交换对象,一个偶数减半后,若参与偶变换的两个数不都是奇数,则不断进行偶变换,否则分配给第三个数(如果已经找到q则永远不再分配给第三个数),继续五。
六、用二进制数表示x/t,在左边补充0直到位数等于k,从最高位到最低位,若为1则将q分配给0,为0则分配给另一个数。这样就得到了x,结束。
至此,我们从理论上推导证明了通解的可行性,此外,我还写了验证该解法的cpp代码,对0<=x<=1000的所有有解数组都进行了验证并且验证成功。
当然,也许还存在其他通解,我很期待看到新想法。
2023数学游戏大闯关 好玩的数学游戏推荐
在我们的日常生活中离不开数学,网上也有很多关于数学的游戏,那么2023数学游戏大闯关有哪些?在游戏中可以帮助玩家开发大脑的思维,还有不同的关卡,可以在这里不断的闯关,下面就是今天小编分享给大家好玩的数学游戏推荐。
1、《数独大全》

这是一款适合任何年龄段的人玩的游戏,在游戏中可以进入数字的天堂,各种不同的关卡设计,还有千变万化的数字,都能让玩家燃烧自己的大脑,在这里可以选择四宫格的数字玩法,随着越来越熟练之后,可以挑战六宫格的数字计算玩法,在每一局当中都需要在规定的时间里完成挑战,可以随着时间的紧迫性,不断的超越自己的极限,在游戏中快速的转动大脑思维。
》》》》》#数独大全#《《《《《
2、《数字运算棋》
这款游戏中可以很好的锻炼玩家的计算能力,在游戏中可以挑战不同难度的关卡,而且每一个关卡当中的玩法都不同,玩家可以操作数字在这里变魔法,运用自己独到的计算能力,可以迅速解答出需要的答案,在这里可以获得极大的成就感,加减乘除任由玩家轻松的玩转,在游戏中可以锻炼自己成为数学小天才。
》》》》》#数字运算棋#《《《《《
3、《宝宝玩数字》

这是一款及其适合小孩子的数学思维游戏,可爱的动画场景可以吸引小朋友的注意力,而且还有教读数字的玩法,在这里可以从最基础的学起,还有可爱的小动物陪伴玩家,通过小朋友去数小母鸡下的蛋等,有趣的游戏互动玩法,可以激发小朋友的兴趣,还有游泳池等不同的主题场景,可以自由的进行切换,在快乐中可以学到很多的知识,在数学小农场当中开启快乐的夏天。
》》》》》#宝宝玩数字#《《《《《
4、《奥特曼学数学》

在这款游戏中给玩家打造了一个生动有趣的学习场景,在这里有小朋友们崇拜的英雄奥特曼,可以随时进行打怪兽,但是每一个关卡当中都要计算出一定得数学题,才可以击败小怪兽,而且还有多个不同难度的等级,在这里可以激发小朋友的胜负欲,快速的掌握计算的方法,营造一个快乐的学习环境。
》》》》》#奥特曼学数学#《《《《《
5、《超级数字》

在这里玩家可以进行轻松的闯关,在游戏中结合了消除和数字的玩法,让玩家能够在游戏中掌握数学知识,还能体会到数学的魅力,每一个关卡当中都有不同难度的数学题,只需要准确的解答成功,就会成功的进行消除,就可以在这里获得一个生命值,每一次答错就会扣除一个生命值,当玩家没有生命值的时候,则会闯关失败。
》》》》》#超级数字#《《《《《
上面这几款游戏就是今天小编分享给大家的2023数学游戏大闯关推荐,在这里玩家可以体验有趣的数学世界,而且还有很多精彩的小游戏,都能轻松的尝试,让玩家可以在数字王国里度过快乐的夏天。
玩枪的乐趣好玩吗 玩枪的乐趣玩法简介
期待已久的手游玩枪的乐趣即将登陆九游,这款手机游戏吸引了大批玩家的关注,想下载这款游戏,有很多粉丝都在问九游小编玩枪的乐趣好玩吗?玩枪的乐趣值不值得玩?现在就为大家来简单分析下,看看这款游戏的玩法特点和游戏剧情介绍 。
玩枪的乐趣快速下载地址(需优先下载九游APP):
》》》》》#玩枪的乐趣#《《《《《
1、玩枪的乐趣简要评析:
2、玩枪的乐趣图片欣赏:
通过上面的游戏介绍和图片,可能大家对玩枪的乐趣有大致的了解了,不过这么游戏要怎么样才能抢先体验到呢?不用担心,目前九游客户端已经开通了测试提醒了,通过在九游APP中搜索“玩枪的乐趣”,点击右边的【订阅】或者是【开测提醒】,订阅游戏就不会错过最先的下载机会了咯!
 全球好游抢先下
全球好游抢先下 福利礼包免费领
福利礼包免费领 官方直播陪你玩
官方直播陪你玩
2022数学游戏有哪些 好玩的数学游戏推荐
数学对于大部分人来说既枯燥又难学,但同时人们又能够在数学游戏中感受到数学的乐趣,于是很多人想要了解2022数学游戏有哪些。事实上,数学游戏不仅能够锻炼人们的逻辑思维能力,也能够提升人们的数学兴趣,今天小编就给大家介绍一些好玩的数学游戏,大家可以根据自己的喜好选择一款。
1、《数字领主》

《数字领主》这个游戏的玩法非常简单,在一张地图上,玩家需要从一个点开始逐渐扩张自己的领土,实现等级的提升。在这其中,并不只有简单的领土扩张,玩家还需要和其他玩家进行对抗,打败对手,感兴趣的玩家快来试试吧!
》》》》》#数字领主#《《《《《
2、《不懂数学》

《不懂数学》这个游戏额规则很简单,玩家需要将数字和运算符号运用起来,最终得到“24”这个数字。看起来好像简单,但事实并非如此,玩家们还是需要发动脑筋好好思考。
》》》》》#不懂数学#《《《《《
3、《极智脑力》
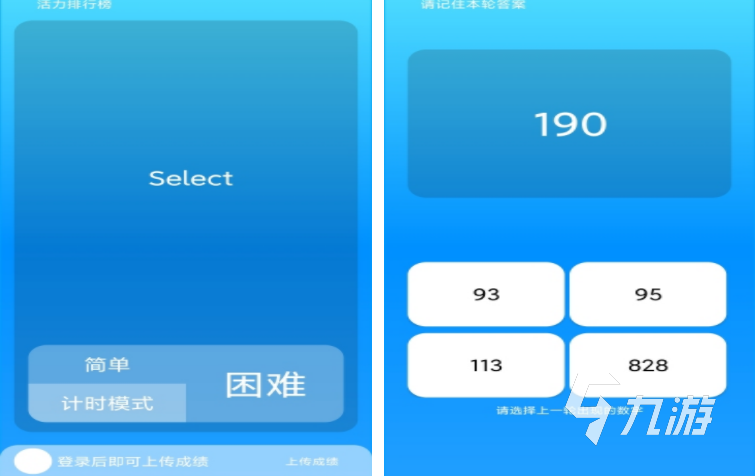
在《极智脑力》游戏中,玩家既能够提升自己的脑力,也可以增强自己的记忆能力,而且游戏还有简单、限时、困难等几种模式,受众广泛,是一款老少皆宜的益智类游戏。
》》》》》#极智脑力#《《《《《
4、《数学迷阵》
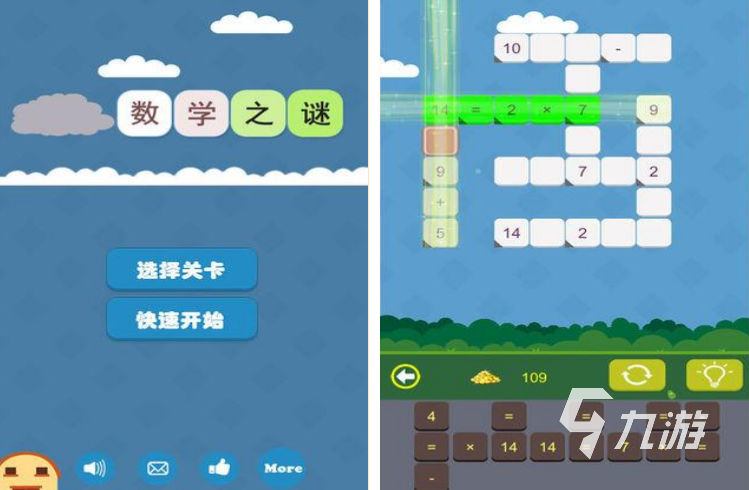
在《数学迷阵》中,玩家需要根据不同的算式来选择对应的方块,规则很简单,但玩起来并没有那么容易,还是不能轻易掉以轻心。这个游戏能够提升玩家的数学能力,以及逻辑思维能力,且游戏中涉及的小学和初中知识,特别适合学生们来巩固数学知识。
》》》》》#数学迷阵#《《《《《
5、《开心数独》

《开心数独》最主要的玩法和《数独》是一样的,只不过其中并非只有九宫格,还有更多类型的宫格,而且级别也很多,从入门到复杂,可以说是老少皆宜。
》》》》》#开心数独#《《《《《
6、《数字华容道数字方块合并》

《数字华容道数字方块合并》这个游戏包含多种益智类的游戏,比如“2048”“扫雷”“数字华容道”等等,玩家们在一个游戏里可以享受到多种游戏玩法,可以说是一种全新的体验。
》》》》》#数字华容道数字方块合并#《《《《《
7、《数学零点HD》
《数学零点HD》这个游戏的规则很简单,就是将数字方块和运算符运用起来,使之等于0,从而使方块全部消失。刚开始的时候数字和运算符都很少,所以很简单,但是玩到后面就会发现越来越难,所以这是一款需要玩家集中注意力,动用脑力的游戏。
》》》》》#数学零点HD #《《《《《
以上就是小编给大家推荐的2022数学游戏有哪些,这一类游戏的画面简单,需要玩家有一定的逻辑能力和思维能力,对数学游戏感兴趣的玩家还在等什么呢?赶紧点击下载来试试看吧!
数学游戏 我爱数学
「我爱数学:MathMathMath」是一款寓教于乐的数学类游戏,画风比较学院,非常适合小朋友玩,在玩游戏的过程中不知不觉学习数学知识,我爱数学,数学使我快乐~
九游括三种模式:
多人游戏:在同一个iPad或者手机上尽快点击正确的答案并收集积分,第一个拿到10分的赢得比赛。
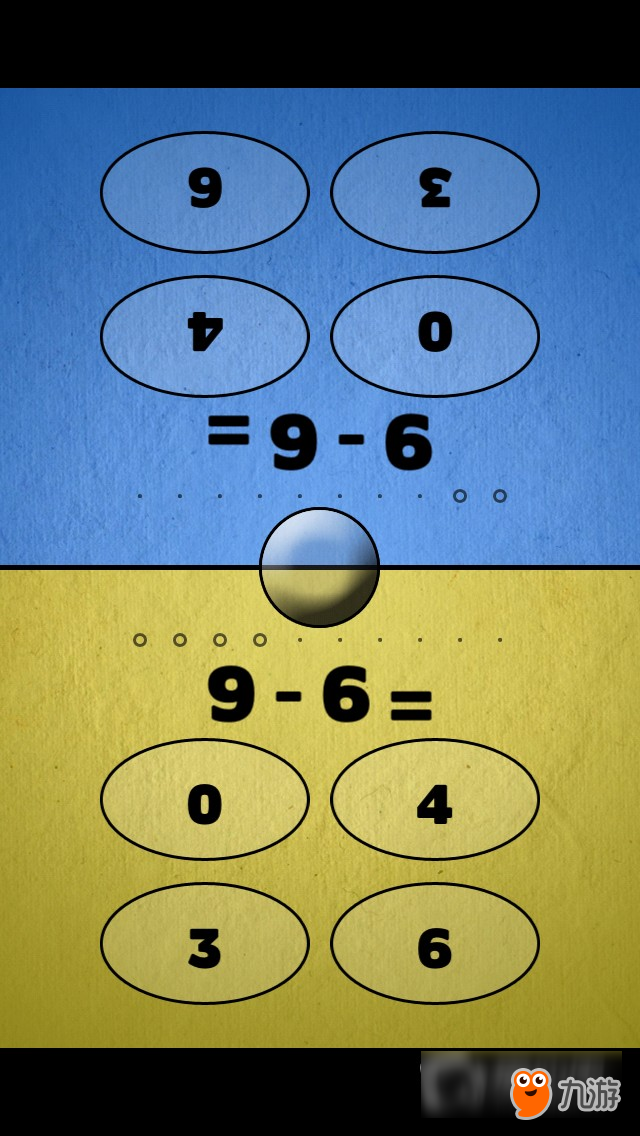
青蛙游戏(单人游戏):点击正确的答案则青蛙就能吃到食物,否则就会失败。
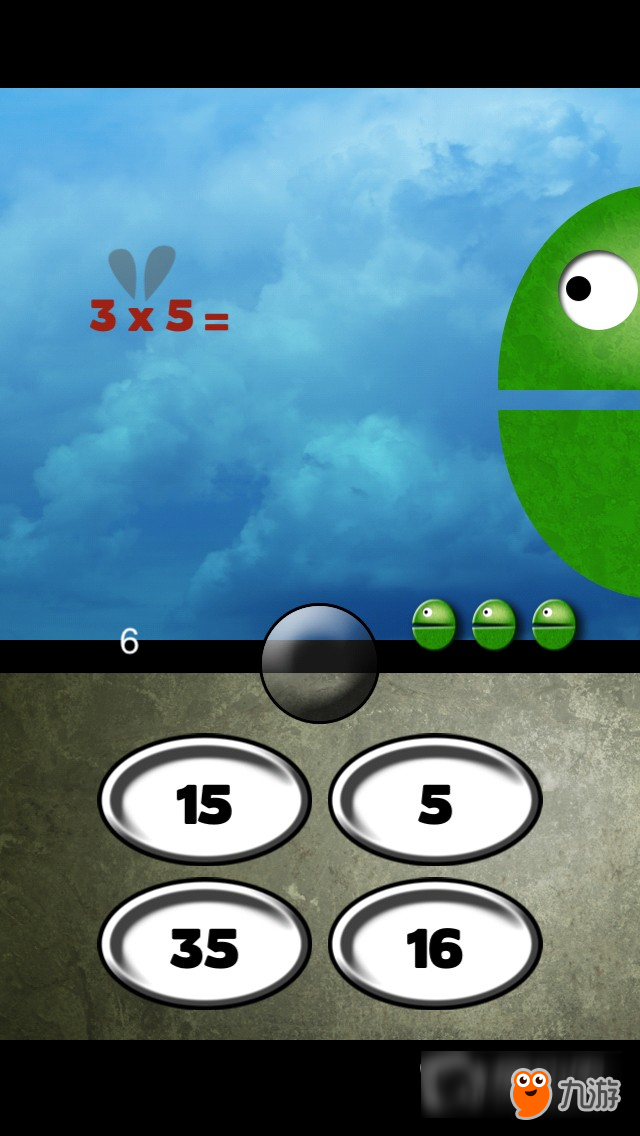
相机游戏(单人游戏):- 同时改善你的健身和你的精神数学技能!游戏可以直接从相机图像中检测出你的动作!在相机前移动,并在空中触摸正确的答案。使用iPad智能外盖将iPad放在直立位置,然后在相机前方跳动,或将设备平放在桌子上,并将其中一根手指移动到相机前方。注意:仅适用于具有正面(面对面)相机的设备(iPad第2代和更新版,iPod第4代及更高版本)。

难得一见的寓教于乐的数学游戏,赶紧下载起来吧~

用2048作数学推算打怪兽 《10BATTLE》带你领略另类RPG乐趣
《10BATTLE》是日本手游厂商 PROPE 在前段时间推出的 RPG 风格小品游戏,本作玩法看似简单,但诸多的教程提示加上只有英文显示这点,即便有在中区上架还是让国内玩家看得一头雾水,不过近日官方正式加入简体中文之后也可顺畅地体验本作的乐趣了。如果还没玩过的话,不妨随同这这篇体验了解一下游戏的魅力吧。

初看画面,《10BATTLE》会给人一种“点点点游戏”的感觉,但实际游玩过后,却变成了《2048》那一类的风格。通过点击同色的方块将其消除,从而结合成新的方块,而消除方块的数量则化为实体数字对敌人造成伤害,同时也会记录在新的方块上。
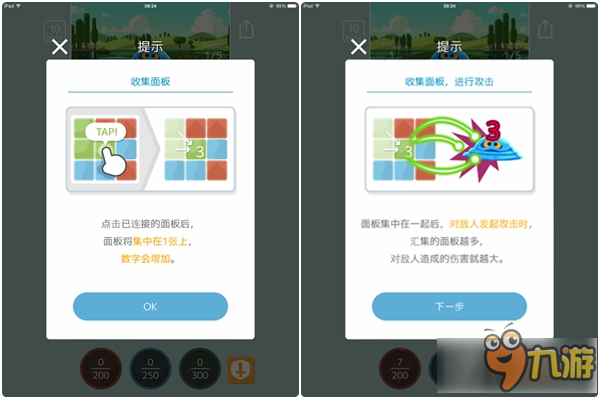
这些数字除了能够累积在方块里以外,还会以能量的形式加载到屏幕下方的技能能量槽中。技能本身也是按照颜色来分类,其对应效果也各有不同,例如一键变为同色或消除指定方块,玩起来颇有三消游戏的氛围。
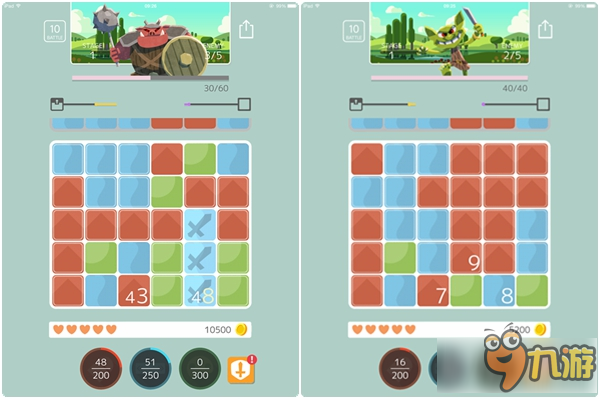
当然游戏的战斗核心并不只是单纯的同色消除合拼这么简单,就如游戏名“10BATTLE”所包含的意义那样,当方块中的数字能够合成 10 的倍数之时,就能够给与怪物更为巨大的伤害,即便是 Boss 级别的血量也能够一击秒杀。
然而如何通过消除合拼的方式让方块数字变成10的倍数则是本作的核心难题,一不小心反而导致自己陷入困境乃是家常便饭的事情。
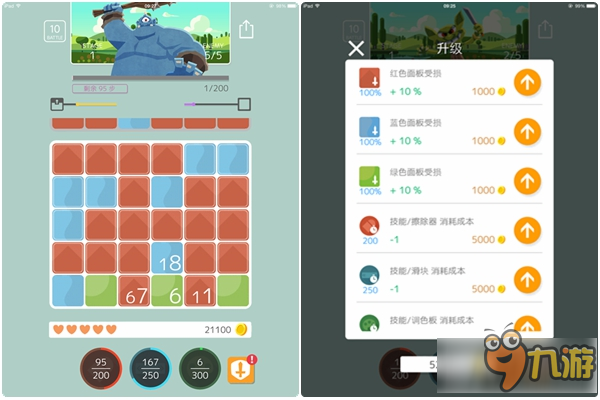
除此之外游戏也设置了一些 RPG 中常见的升级元素,例如同色方块伤害提升、技能消耗减少等,通过打怪赚取的金币便可进行相应提升。即使是拥有过人的消除技巧,伤害上不去的话,到了往后关卡还是较为吃力,所以金币可不要留着,一口气强化到最佳状态吧。
《10BATTLE》本身融合了不少类型的元素,但实际的游玩过程却是相当单纯,如何消除才能组合更高的数字达成 10 倍数的最大利益化也是很考验玩家的思维能力,再加上中文的支持使得游戏介绍变得简单易懂,如果你当初因为看不懂而放弃本作的话,那么现在可是重拾本作的最好机会了。
如转载涉及版权等问题,请作者与我司联系,我司将在第一时间删除或支付稿酬。
数学的乐趣同类推荐
相关专题
最新专题
- 免费碰碰游戏有什么2024
- 画风独特的游戏有哪些
- 手机上有没有火车拼图游戏
- 第七幻域公测版下载地址推荐
- 探号账号交易软件怎么样
- 修仙掌门模拟器下载地址
- 斗罗大陆逆转时空测试服下载地址
- 猫咪和汤怎么预约
- 物华弥新下载链接分享
- 归龙潮下载链接推荐
- 神庙逃亡2下载安装免费
- 洛克人11免费下载地址
- 好玩的火影手游有哪些
- 解压数字游戏下载分享2024
- 解压连连看游戏免费推荐
- 全国手游排行榜前十名有哪些
- 换装3d游戏有哪些
- 联机恐怖解密手游有哪些
- 2024有趣的汽车停车处游戏合集
- 2024儿童三人游戏有哪些
- 流行的金字塔经营游戏下载排行
- 跑车模拟游戏分享2024
- 经典的儿童益智游戏有哪些
- 2024热门的美少女枪战游戏有哪些
- 好玩横版的手游有哪些
- 欧美格斗游戏有哪些
- 有趣的国外多人游戏推荐
- 科幻第一人称射击游戏推荐
- 2024忍者横版过关游戏推荐
- 2024有趣的经营烹饪游戏有哪些
游戏排行


即将上线










最新游戏
最新资讯















































 粤公网安备44010602000283号
粤公网安备44010602000283号
